题目内容
如图,已知双曲线 与直线
与直线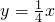 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线 于点E,交BD于点C.
于点E,交BD于点C.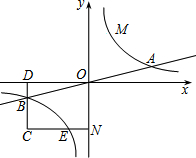
(1)若点A坐标是(8,2),求B点坐标及反比例函数解析式.
(2)过A点作AQ垂直于y轴交于Q点,设P点从D点出发沿D→C→N路线以1个单位长度的速度运动,DC长为4.求△AQP的面积S与运动时间t的关系式,并求出S的最大值.
(3)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
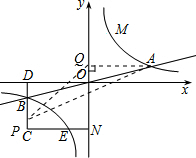 解:(1)∵点A坐标是(8,2),
解:(1)∵点A坐标是(8,2),∴B点坐标为(-8,-2).
∴k=xy=-8×(-2)=16,
∴y=
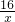 ;
;(2)过A点作AQ垂直于y轴交于Q点,
设P点从D点出发延D→C→N路线以1个单位长度的速度运动,DC长为4,
∵点A坐标是(8,2),
∴AQ=8,DP=t,QN=6,
∴当0≤t≤4时,
S=
 t×AQ=4t,
t×AQ=4t,当4≤t≤10时,
S=
 ×QN×AQ=
×QN×AQ= ×8×6=24;
×8×6=24;∴△AQP的面积S与运动时间t的关系式为:
 ;
;∴S的最大值为24;
(3)设B点坐标为(x1,-
 ),代入y=
),代入y= x得,-
x得,- =
= x1,x1=-2n;
x1,x1=-2n;∴B点坐标为(-2n,-
 ).
).因为BD∥y轴,所以C点坐标为(-2n,-n).
因为四边形ODCN的面积为2n•n=2n2,三角形ODB,三角形OEN的面积均为
 ,四边形OBCE的面积为4.
,四边形OBCE的面积为4.则有2n2-k=4 ①;

又因为2n•
 =k,即n2=k ②
=k,即n2=k ②②代入①得,4=2k-k,解得k=4;则解析式为y=
 ;
;又因为n2=4,故n=2或n=-2.
M在第一象限,n>0;
将M(m,2)代入解析式y=
 ,得m=2.故M点坐标为(2,2);C(-4,-2);
,得m=2.故M点坐标为(2,2);C(-4,-2);设直线CM解析式为y=kx+b,则
 ,
,解得
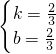
∴一次函数解析式为:y=
 x+
x+ .
.分析:(1)根据A点的横坐标为(8,2),A、B两点关于原点对称,易得k的值;
(2)利用A,B两点的坐标得出AQ,CN的长,利用P在CD上和P在CN上分别得出即可,进而得出面积最值即可;
(3)根据S矩形DCNO=2mn=2k,S△DBO=
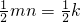 ,S△OEN=
,S△OEN=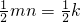 ,即可得出k的值,进而得出B,C点的坐标,再求出解析式即可.
,即可得出k的值,进而得出B,C点的坐标,再求出解析式即可.点评:此题主要考查了待定系数法函数解析式以及一次函数与反比例函数交点的性质,根据四边形OBCE的面积为4得出k的值是解决问题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 探索函数
探索函数 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直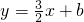 与双曲线
与双曲线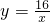 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.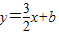 与双曲线
与双曲线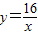 相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.
相交于第一象限内的点A,AB、AC分别垂直于x轴、y轴,垂足分别为B、C,已知四边形ABCD是正方形,求直线所对应的一次函数的解析式以及它与x轴的交点E的坐标.