题目内容
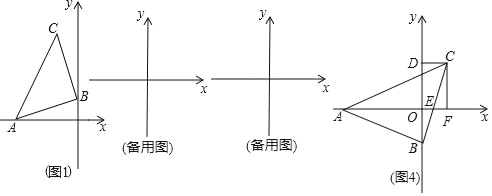
【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).
【答案】(1)C(﹣1,4);(2)OD=a﹣b;(3)aAE+bCF=﹣a(a+b).
【解析】
(1)先确定出OA=3,OB=1,进而判断出△AOB≌△BDC,即可得出BD=3,CD=1,即可得出结论;
(2)分三种情况,同(1)的方法即可得出结论;
(3)先确定出OF=CD=﹣b,CF=OD=b﹣a,进而得出AF=OA+OF=﹣a﹣b,在判断出△AOB∽△CFE,即可得出EF=![]() (b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣
(b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),即可得出结论.
(b﹣a),即可得出结论.
解:(1)如图1,
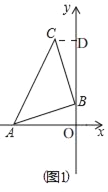
∵点A的坐标为(﹣3,0),点B的坐标为(0,1),
∴OA=3,OB=1,
过点C作CD⊥y轴于D,
∴∠BCD+∠CBD=90°,
∵∠ABC=90°,
∴∠CBD+∠ABO=90°,
∴∠ABO=∠BCD,
在△AOB和△BDC中,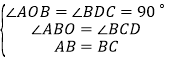 ,
,
∴△AOB≌△BDC,
∴BD=OA=3,CD=OB=1,
∴OD=OB+BD=4,
∴C(﹣1,4);
(2)当点B在y轴正半轴上时,
如图1,∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=b,
∴OD=OB+BD=b+(﹣a)=b﹣a,
当点B在y轴负半轴上,点C在第一象限时,如图2,
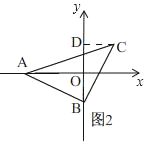
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
当点B在y轴负半轴,点C在第四象限时,如图3,

∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=OB﹣BD=﹣b﹣(﹣a)=a﹣b;
(3)如图4,
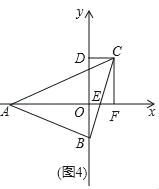
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
∵CF⊥OA于F,
∴四边形ODCF是矩形,
∴OF=CD=﹣b,CF=OD=b﹣a,
∴AF=OA+OF=﹣a﹣b,
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵AF平分∠BAC,
∴∠OAC=∠OAB=22.5°,
∴∠ECF=∠ACF﹣∠ACB=90°﹣∠OAC﹣∠ACB=22.5°=∠OAB,
∵∠AOB=∠CFE,
∴△AOB∽△CFE,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() (b﹣a),
(b﹣a),
∴AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),
(b﹣a),
∵CF=b﹣a,
∴AE=﹣a﹣b﹣![]() CF,
CF,
∴aAE+bCF=﹣a(a+b).

【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.