题目内容
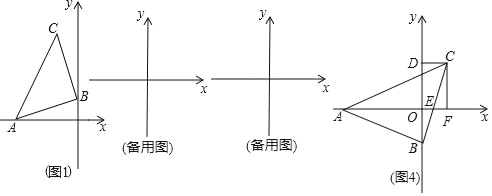
【题目】某文具店到批发市场选购A、B两种文具,批发价分别为14元/个、10元/个.若该店零售A、B两种文具的每天销量y(个)与零售价x(元/个)都是一次函数y=kx+20的关系,如图所示. 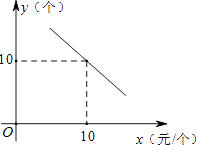
(1)求此一次函数的关系式;
(2)现批发市场进行促销活动,凭会员卡(240元/张)在该批发市场购买所有物品均进行打折优惠,若文具店购买A、B两种文具各50个,问打折小于多少折时,采用购买会员卡的方式合算;
(3)在文具店不购买会员卡的情况下,若A种文具零售价比B种文具零售价高2元/个,求这两种文具每天的销售总利润W(元)与A种文具零售价x(元/个)之间的函数关系式,并说明当A种文具的零售价为多少时,每天的销售利润最大. (说明:本题不要求写出自变量x的取值范围)
【答案】
(1)解:根据题意得出,把(10,10)代入y=kx+20,得10=10k+20,
解得:k=﹣1.
故一次函数解析式为:y=﹣x+20;
(2)解:设打折为a折时,购买会员卡的方式合算,依据题意得出:
240+50×14×0.1a+50×10×0.1a<50×14+50×10,
解得:a<8.
答:打折小于8折时,采用购买会员卡的方式合算;
(3)解:A种文具零售价为x(元/个),根据题意得出:
W=(x﹣14)(﹣x+20)+(x﹣2﹣10)[﹣(x﹣2)+20]=﹣2(x﹣17)2+34,
故当x=17时,每天的销售利润最大.
【解析】(1)先设出一次函数,根据图形中的关系利用待定系数法求出关系式.(2)根据题意设打折为a折时,购买会员卡的方式合算,由题中已知条件列出不等式,求出a即可.(3)首先得出y与x的函数关系,再运用配方法求出二次函数的对称轴,由函数性质求解.

【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图: 根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析: ①从平均数和中位数方面比较一班和二班的成绩;②从平均数和众数方面比较一班和二班的成绩;③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.