Question

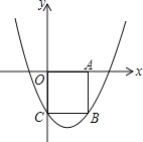
【题目】（1）问题发现：如图①，正方形AEFG的两边分别在正方形ABCD的边AB和AD上，连接CF.

①写出线段CF与DG的数量关系；

②写出直线CF与DG所夹锐角的度数.

（2）拓展探究：

如图②，将正方形AEFG绕点A逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明.

（2）问题解决

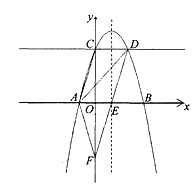
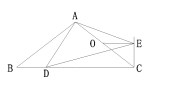
如图③，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC=4，O为AC的中点.若点D在直线BC上运动，连接OE，则在点D的运动过程中，线段OE的长的最小值.（直接写出结果）

Answer 1

【答案】（1）①易得CF=DG;②45；

(2) （1）中的结论仍然成立,证明见详解；

(3).

【解析】

（1）①易得CF=DG;

②45；

(2) 连接AC、AF,在正方形ABCD中，可得△CAF∽DAG，=,CF=DG，

在△CHD中，∠CHD=180-135=45，（1）中的结论是否仍然成立；

（3）OE⊥CE时，OE最短，此时OE=CE,△OEC为等腰直角三角形，OC=AC=2,可得OE的值.

（1）①易得CF=DG;

②45；

(2)①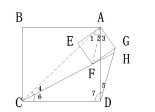

连接AC、AF,在正方形ABCD中，延长CF交DG与H点，

∠CAD=∠BCD=45,

设AD=CD=a，易得AC=a=AD,

同理在正方形AEFG中，∠FAG=45,AF=AG,

∠CAD=∠FAG, ∠CAD-∠2=∠FAG-∠2,

∠1=∠3

又

△CAF∽DAG,

=,CF=DG;

②由△CAF∽DAG，∠4=∠5，

∠ACD=∠4+∠6=45, ∠5+∠6=45，

∠5+∠6+∠7=135，

在△CHD中，∠CHD=180-135=45，

（1）中的结论是否仍然成立

（3）

由∠BAC=∠DAE=90,可得∠BAD=∠CAE,又AB=AC,AD=AE,

可得△BAD≌△CAE,

∠ACE=∠ABC=45,

又∠ACB=45,∠BCE=90,即CE⊥BC,

根据点到直线的距离垂线段最短，

OE⊥CE时，OE最短，此时OE=CE,△OEC为等腰直角三角形，

OC=AC=2,

由等腰直角三角形性质易得，OE=，

OE的最小值为.