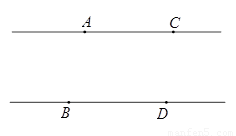题目内容
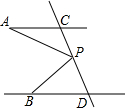 如图,AC∥BD,点P在直线CD上.
如图,AC∥BD,点P在直线CD上.
(1)∠PAC,∠APB,∠PBD有什么关系,并说明理由.
(2)当点P移动到线段DC的延长线上时,它们之间又有什么关系?画出图形并说明理由.
(1)解:
∠APB=∠PAC+∠PBD,
理由是:过P作PQ∥AC,
∵AC∥BD,
∴AC∥PQ∥BD,
∴∠APQ=∠PAC,∠BPQ=∠PBD,
∴∠APB=∠APQ+∠BPQ=∠PAC+∠PBD;
(2)解:∠APB=∠PBD-∠PAC,
理由是:过P作PQ∥AC,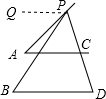
∵AC∥BD,
∴AC∥PQ∥BD,
∴∠APQ=∠PAC,∠BPQ=∠PBD,
∴∠APB=∠BPQ-∠APQ=∠PBD-∠PAC.
分析:(1)∠APB=∠PAC+∠PBD,理由是:过P作PQ∥AC,根据AC∥PQ∥BD推出∠APQ=∠PAC,∠BPQ=∠PBD,代入∠APB=∠APQ+∠BPQ即可;
(2)∠APB=∠PBD-∠PAC,理由是:过P作PQ∥AC,根据平行线性质得出∠APQ=∠PAC,∠BPQ=∠PBD,代入∠APB=∠BPQ-∠APQ求出即可.
点评:本题考查了平行线性质的应用,注意:两直线平行线,内错角相等.

∠APB=∠PAC+∠PBD,
理由是:过P作PQ∥AC,
∵AC∥BD,
∴AC∥PQ∥BD,
∴∠APQ=∠PAC,∠BPQ=∠PBD,
∴∠APB=∠APQ+∠BPQ=∠PAC+∠PBD;
(2)解:∠APB=∠PBD-∠PAC,
理由是:过P作PQ∥AC,

∵AC∥BD,
∴AC∥PQ∥BD,
∴∠APQ=∠PAC,∠BPQ=∠PBD,
∴∠APB=∠BPQ-∠APQ=∠PBD-∠PAC.
分析:(1)∠APB=∠PAC+∠PBD,理由是:过P作PQ∥AC,根据AC∥PQ∥BD推出∠APQ=∠PAC,∠BPQ=∠PBD,代入∠APB=∠APQ+∠BPQ即可;
(2)∠APB=∠PBD-∠PAC,理由是:过P作PQ∥AC,根据平行线性质得出∠APQ=∠PAC,∠BPQ=∠PBD,代入∠APB=∠BPQ-∠APQ求出即可.
点评:本题考查了平行线性质的应用,注意:两直线平行线,内错角相等.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 12、如图,AC⊥BD于点C,DE⊥AB于点E,且AB=6,DB=8,则S△ABC:S△DBE=
12、如图,AC⊥BD于点C,DE⊥AB于点E,且AB=6,DB=8,则S△ABC:S△DBE= 如图,AC∥BD,点E在线AD的延长线上,∠A=30°,则∠BDE的度数为( )
如图,AC∥BD,点E在线AD的延长线上,∠A=30°,则∠BDE的度数为( ) 如图,AC∥BD,点P在直线CD上.
如图,AC∥BD,点P在直线CD上.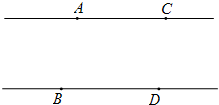 如图,AC∥BD,点P是直线AC和BD之间的一动点,当点P运动到某一位置时,连接PA,PB.
如图,AC∥BD,点P是直线AC和BD之间的一动点,当点P运动到某一位置时,连接PA,PB.