Question

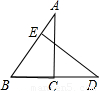
12、如图，AC⊥BD于点C，DE⊥AB于点E，且AB=6，DB=8，则S_△ABC：S_△DBE=

9：16

．

Answer 1

分析：首先证明△ABC∽△DBE，然后根据相似三角形的面积比等于相似比的平方，即可得出两个相似三角形的面积比．

解答：解：∵∠DEB=∠ACB=90°，∠B=∠B，
∴△ABC∽△DBE；
又∵AB=6，DB=8，根据相似三角形的面积比等于相似比的平方，
∴S_△ABC：S_△DBE=AB²：BD²=9：16．

点评：此题主要考查的是相似三角形的性质：相似三角形的对应边的比等于相似比，面积比等于相似比的平方．