Question

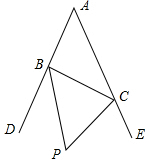
如图，在△ABC中，∠A=60°，DB、CD分别是∠ABC、∠ACB的角分线，BE、EC分别是∠DBC、∠DCB的角分线，则∠BEC的度数是______．

Answer 1

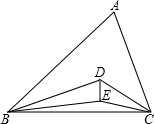
在△ABC中，∠A=60°，
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°，
∵DB、CD分别是∠ABC、∠ACB的角分线，
∴∠DBC+∠DCB=

1

2

∠ABC+

1

2

∠ACB=

1

2

（∠ABC+∠ACB）=

1

2

×120°=60°，
同理：∠EBC+∠ECB=

1

2

（∠DBC+∠DCB）=

1

2

×60°=30°，
∴∠BEC=180°-（∠EBC+∠ECB）=180°-30°=150°，
故答案为：150°．