题目内容
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t< ![]() ).
). 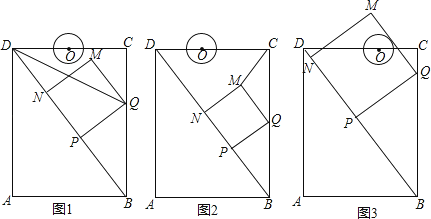
(1)如图1,连接DQ平分∠BDC时,t的值为;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
【答案】
(1)![]()
(2)
解:解:如图2中,作MT⊥BC于T.
∵MC=MQ,MT⊥CQ,
∴TC=TQ,
由(1)可知TQ= ![]() (8﹣5t),QM=3t,
(8﹣5t),QM=3t,
∵MQ∥BD,
∴∠MQT=∠DBC,
∵∠MTQ=∠BCD=90°,
∴△QTM∽△BCD,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() (s),
(s),
∴t= ![]() s时,△CMQ是以CQ为底的等腰三角形
s时,△CMQ是以CQ为底的等腰三角形
(3)
解:①证明:如图2中,由此QM交CD于E,
∵EQ∥BD,
∴ ![]() =
= ![]() ,
,
∴EC= ![]() (8﹣5t),ED=DC﹣EC=6﹣
(8﹣5t),ED=DC﹣EC=6﹣ ![]() (8﹣5t)=
(8﹣5t)= ![]() t,
t,
∵DO=3t,
∴DE﹣DO= ![]() t﹣3t=
t﹣3t= ![]() t>0,
t>0,
∴点O在直线QM左侧.
②解:如图3中,由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E.
∵EC= ![]() (8﹣5t),DO=3t,
(8﹣5t),DO=3t,
∴OE=6﹣3t﹣ ![]() (8﹣5t)=
(8﹣5t)= ![]() t,
t,
∵OH⊥MQ,
∴∠OHE=90°,
∵∠HEO=∠CEQ,
∴∠HOE=∠CQE=∠CBD,
∵∠OHE=∠C=90°,
∴△OHE∽△BCD,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() .
.
∴t= ![]() s时,⊙O与直线QM相切.
s时,⊙O与直线QM相切.
连接PM,假设PM与⊙O相切,则∠OMH= ![]() PMQ=22.5°,
PMQ=22.5°,
在MH上取一点F,使得MF=FO,则∠FMO=∠FOM=22.5°,
∴∠OFH=∠FOH=45°,
∴OH=FH=0.8,FO=FM=0.8 ![]() ,
,
∴MH=0.8( ![]() +1),
+1),
由 ![]() 得到HE=
得到HE= ![]() ,
,
由 ![]() 得到EQ=
得到EQ= ![]() ,
,
∴MH=MQ﹣HE﹣EQ=4﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴0.8( ![]() +1)≠
+1)≠ ![]() ,矛盾,
,矛盾,
∴假设不成立.
∴直线MQ与⊙O不相切.
【解析】(1)解:如图1中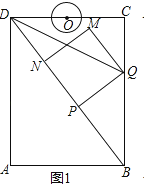 ,
,
∵四边形ABCD是矩形,
∴∠A=∠C=∠ADC=∠ABC=90°,AB=CD=6.AD=BC=8,
∴BD= ![]() =
= ![]() =10,
=10,
∵PQ⊥BD,
∴∠BPQ=90°=∠C,
∵∠PBQ=∠DBC,
∴△PBQ∽△CBD,
∴ ![]() ,
,
∴ ![]() ,
,
∴PQ=3t,BQ=5t,
∵DQ平分∠BDC,QP⊥DB,QC⊥DC,
∴QP=QC,
∴3t=6﹣5t,
∴t= ![]() ,
,
所以答案是 ![]() .
.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
【题目】某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整). 学生投票结果统计表
候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
得票数 | 200 | 300 |
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?