题目内容
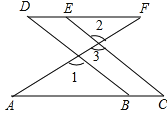
【题目】如图所示,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,求证:∠A=∠F.
【答案】因为∠l=∠2(已知)
∠2=∠3(对顶角相等)
所以∠l=∠3(等量代换)………………………………………………………2分
所以BD∥CE(同位角相等,两直线平行)……………………………………4分
所以∠C=∠DBA(两直线平行,同位角相等)………………………………6分
又因为∠C=∠D(已知)
所以∠DBA=∠D(等量代换)…………………………………………………8分
所以DF∥AC(内错角相等,两直线平行)………………………………………9分
所以∠A=∠F(两直线平行,内错角相等)…………………………………………10分
【解析】试题分析:根据对顶角的性质得到BD∥CE的条件,然后根据平行线的性质得到∠B=∠C,已知∠C=∠D,则得到满足AB∥EF的条件,再根据两直线平行,内错角相等得到∠A=∠F.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AB∥EF,
∴∠A=∠F.

【题目】盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒子里摇匀再摸.在摸球活动中得到下列表中部分数据.
摸球次数 | 出现红球的频数 | 出现红球的频率 | 摸球次数 | 出现红球的频数 | 出现红球的频率 |
50 | 17 | 34% | 350 | 103 | 29.4% |
100 | 32 | 32% | 400 | 123 | |
150 | 44 | 29.3% | 450 | 136 | 30.2% |
200 | 64 | 32% | 500 | 148 | 29.6% |
250 | 78 | 31.2% | 550 | 167 | |
300 | 32% | 600 | 181 | 30.2% |
(1)请将表中数据补充完整.
(2)画出出现红球的频率的折线统计图.
(3)观察所画折线统计图,你发现了什么?
(4)你认为盒子里哪种颜色的球多?
(5)如果从盒子里任意摸出一球,你认为摸到白球的概率有多大?




