题目内容
【题目】有A、B两种饮料,这两种饮料的体积和单价如表:
类型 | A | B |
单瓶饮料体积/升 | 1 | 2.5 |
单价/元 | 3 | 4 |
(1)小明购买A、B两种饮料共13升,用了25元,他购买A,B两种饮料个各多少瓶?
(2)若购买A、B两种饮料共36瓶,且A种饮料的数量不多于B种饮料的数量,则最少可以购买多少升饮料?
【答案】
(1)解:设他购买了A种饮料a瓶,B种饮料b瓶.
则由题意可得 ![]() ,
,
解得 ![]() .
.
故他购买了3瓶A种饮料,4瓶B种饮料;
(2)解:设购买了A种饮料x瓶,购买了y升饮料,
则x≥0且x≤36﹣x,解得0≤x≤18,
由题意可得y=x+2.5(36﹣x)﹣﹣1.5x+90,
∵﹣1.5<0,
∴y随的增大而减小,
当x=18时,ymin=﹣1.5×18+90=63.
∴最少可以购买63升饮料
【解析】(1)设他购买了A种饮料a瓶,B种饮料b瓶,根据“购买A、B两种饮料共13升;用了25元”列方程组求解即可;(2)设购买了A种饮料x瓶,购买了y升饮料,首先确定自变量的取值范围,然后得到有关饮料总升和饮料瓶数之间的关系得到函数解析式,确定函数的最值即可.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案【题目】如图,一扇窗户,窗框为铝合金材料,下面是由两个大小相等的长方形窗框构成,上面是由三个大小相等的扇形组成的半圆窗框构成,窗户半圆部分安装彩色玻璃,两个长方形部分安装透明玻璃(本题中π取3,长度单位为米).
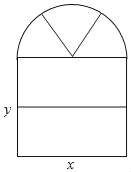
(1)一扇这样窗户一共需要铝合金多少米?(用含x,y的代数式表示)
(2)一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含x,y的代数式表示)
(3)某公司需要购进20扇窗户,在同等质量的前提下,甲、乙两个厂商分别给出如下报价:
铝合金(米/元) | 彩色玻璃(平方米/元) | 透明玻璃(平方米/元) | |
甲厂商 | 200 | 80 | 不超过100平方米的部分,90元/平方米,超过100平方米的部分,70元/平方米 |
乙厂商 | 220 | 60 | 80元/平方米,每购1平方米透明玻璃送0.1米铝合金 |
当x=2,y=3时,该公司在哪家厂商购买窗户合算?