题目内容
先阅读后解题.
已知m2+2m+n2-6n+10=0,求m和n的值
解:把等式的左边分解因式:(m2+2m+1)+(n2-6n+9)=0
即(m+1)2+(n-3)2=0
因为(m+1)2≥0,(n-3)2≥0
所以m+1=0,n-3=0即m=-1,n=3.
利用以上解法,解下列问题:已知:x2-4x+y2+y+ =0,求x和y的值.
=0,求x和y的值.
解:把等式左边变形:(x2-4x+4)+(y2+y+ )=0,
)=0,
即(x-2)2+(y+ )2=0,
)2=0,
∵(x-2)2≥0,(y+ )2≥0,
)2≥0,
∴x-2=0,y+ =0,
=0,
∴x=2,y= .
.
分析:先把等式左边变形得到两个完全平方式,即(x-2)2+(y+ )2=0,再根据几个非负数的和的性质得到x-2=0,y+
)2=0,再根据几个非负数的和的性质得到x-2=0,y+ =0,然后解两个一次方程即可.
=0,然后解两个一次方程即可.
点评:本题考查了因式分解的应用:把所求的代数式运用因式分解进行变形,然后利用整体思想进行计算.也考查了非负数的性质.
 )=0,
)=0,即(x-2)2+(y+
 )2=0,
)2=0,∵(x-2)2≥0,(y+
 )2≥0,
)2≥0,∴x-2=0,y+
 =0,
=0,∴x=2,y=
 .
.分析:先把等式左边变形得到两个完全平方式,即(x-2)2+(y+
 )2=0,再根据几个非负数的和的性质得到x-2=0,y+
)2=0,再根据几个非负数的和的性质得到x-2=0,y+ =0,然后解两个一次方程即可.
=0,然后解两个一次方程即可.点评:本题考查了因式分解的应用:把所求的代数式运用因式分解进行变形,然后利用整体思想进行计算.也考查了非负数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
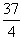 =0,求x和y的值。
=0,求x和y的值。