题目内容
先阅读后解题
若m2+2m+n2-6n+10=0,求m和n的值.
解:m2+2m+1+n2-6n+9=0
即(m+1)2+(n-3)2=0
∵(m+1)2≥0,(n-3)2≥0
∴(m+1)2=0,(n-3)2=0
∴m+1=0,n-3=0
∴m=-1,n=3
利用以上解法,解下列问题:
已知 x2+5y2-4xy+2y+1=0,求x和y的值.
解:∵x2+5y2-4xy+2y+1=0,
∴(x-2y)2+(y+1)2=0,
∴x-2y=0,y+1=0,
x=-2,y=-1.
分析:由x2+5y2-4xy+2y+1=0,可得(x-2y)2+(y+1)2=0,根据非负数的性质即可求出x、y的值.
点评:本题考查了配方法的应用及二元一次方程组的解法,难度一般,关键是注意配方法的步骤.注意在变形的过程中不要改变式子的值.
∴(x-2y)2+(y+1)2=0,
∴x-2y=0,y+1=0,
x=-2,y=-1.
分析:由x2+5y2-4xy+2y+1=0,可得(x-2y)2+(y+1)2=0,根据非负数的性质即可求出x、y的值.
点评:本题考查了配方法的应用及二元一次方程组的解法,难度一般,关键是注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
相关题目
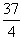 =0,求x和y的值。
=0,求x和y的值。