��Ŀ����
����Ŀ�������ַ���֤���������ε���Ǻ͵���360�㡱��
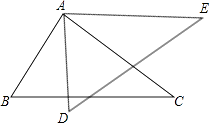
��ͼ����BAE����CBF����ACD����ABC��������ǣ�
��֤��BAE+��CBF+��ACD=360�㣮
֤��1���� �����BAE+��1+��CBF+��2+��ACD+��3=180����3=540��
���BAE+��CBF+��ACD=540�㩁����1+��2+��3����
�� �����BAE+��CBF+��ACD=540�㩁180��=360�㣮
���֤��1�������������ò�ͬ�ķ������֤��2��
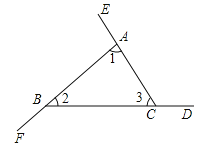
���𰸡�ƽ�ǵ���180�㣬��1+��2+��3=180�㣮
��������
���������֤��1������ƽ�ǵĶ���õ���BAE+��1+��CBF+��2+��ACD+��3=540�㣬�ٸ����������ڽǺͶ����ͽǵĺͲ��ϵ���ɵõ����ۣ�
֤��2��Ҫ��֤��BAE+��CBF+��ACD=360�㣬����������������ʵõ���BAE=��2+��3����CBF=��1+��3����ACD=��1+��2������BAE+��CBF+��ACD=2����1+��2+��3����Ȼ������������ڽǺͶ������ɵõ����ۣ�
���������֤��1����ƽ�ǵ���180�㣬���BAE+��1+��CBF+��2+��ACD+��3=180����3=540�㣬���BAE+��CBF+��ACD=540�㩁����1+��2+��3����
�ߡ�1+��2+��3=180�㣬���BAE+��CBF+��ACD=540�㩁180��=360�㣮
֤��2���ߡ�BAE=��2+��3����CBF=��1+��3����ACD=��1+��2�����BAE+��CBF+��ACD=2����1+��2+��3�����ߡ�1+��2+��3=180�㣬���BAE+��CBF+��ACD=360�㣮
�ʴ�Ϊ��ƽ�ǵ���180�㣬��1+��2+��3=180�㣮

 ��У����ϵ�д�
��У����ϵ�д�