题目内容
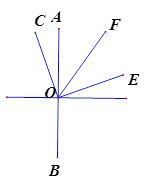
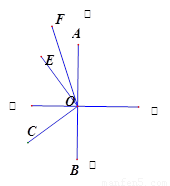
已知:0为直线AB上的一点,射线OA表示正北方向,射线OC在北偏东m°的方向,射线OE在南偏东n°的方向,射线OF平分∠AOE,且2m+2n=180.
(1)如图1,∠ COE=______°, ∠COF和∠BOE之间的数量关系为________________.
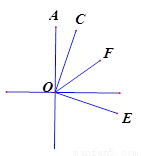
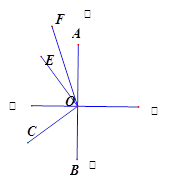
(2)若将∠COE绕点O旋转至图2的位置,射线OF仍然平分∠AOE时,试问(1)中∠COF和∠BOE之间的数量关系是否发生变化?若不发生变化,请你加以证明,若发生变化,请你说明理由;

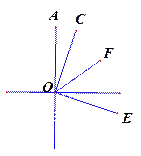
(3)若将∠COE绕点0旋转至图3位置,射线OF仍平分∠AOE时,则2 ∠COF+∠BOE= _°.
【答案】
(1)90,∠BOE=2∠COF
(2)证明略
(3)360
【解析】解:(1)90,∠BOE=2∠COF; ……4分
(2)不发生变化.证明如下:
∠COF=90°-∠EOF ……5分
=90°-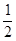 ∠AOE
……6分
∠AOE
……6分
=90°-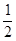 (180°-∠BOE)
(180°-∠BOE)
=90°-90°+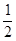 ∠BOE
∠BOE
=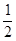 ∠BOE
……7分
∠BOE
……7分
∴∠BOE=2∠COF ……8分
(3)360. ……10分

练习册系列答案
相关题目
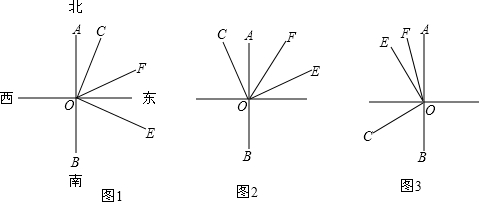
 如图,已知点O为直线AB上一点,射线OA、OB分别平分∠COD和∠EOF.
如图,已知点O为直线AB上一点,射线OA、OB分别平分∠COD和∠EOF.