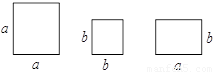
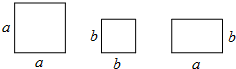
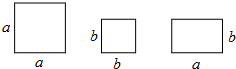题目内容
23、分别画出如图所示几何体的三视图，并求几何体的表面积和体积．
分析：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形；计算表面积找到所有面的和相加即可；所给几何体的体积均为相应的底面积乘高，把相关数值代入即可求解．
解答：解：①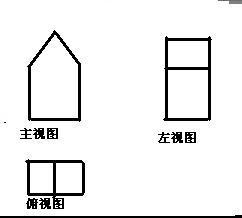
由勾股定理易得主视图中等腰三角形的腰长为5cm，
表面积为：6×2×2+8×2×2+2×6×4÷2+2×5×8+6×8═208cm2；
体积为：（6×2+6×4÷2）×8=192cm3；
②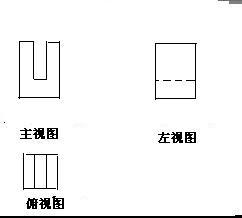
表面积为：9×4.5×2+4.5×9×2+（4.5×4.5-1.5×3）×2+3×9×2=247.5cm2；
体积为：（4.5×4.5-1.5×3）×9=141.75cm3；
③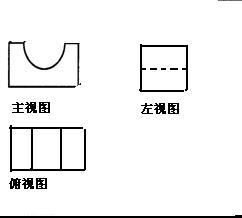
表面积为：15×5×2+10×15+2×（10×5-π×32）+（6π+4）×15=（460+72π）cm2；
体积为：（10×5-π×32）×15=（750-135π）cm3．
由勾股定理易得主视图中等腰三角形的腰长为5cm，表面积为：6×2×2+8×2×2+2×6×4÷2+2×5×8+6×8═208cm2；
体积为：（6×2+6×4÷2）×8=192cm3；
②
表面积为：9×4.5×2+4.5×9×2+（4.5×4.5-1.5×3）×2+3×9×2=247.5cm2；
体积为：（4.5×4.5-1.5×3）×9=141.75cm3；
③
表面积为：15×5×2+10×15+2×（10×5-π×32）+（6π+4）×15=（460+72π）cm2；
体积为：（10×5-π×32）×15=（750-135π）cm3．
点评：解决本题的关键是理解三视图的定义，注意表面积的求法，以及均匀几何体的体积的求法；易错点是得到几何体所有的表面积．
练习册系列答案
相关题目
