题目内容
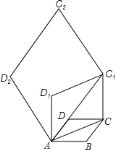
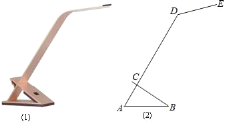
【题目】如图![]() ,分别沿长方形纸片
,分别沿长方形纸片![]() 和正方形纸片
和正方形纸片![]() 的对角线
的对角线![]() ,
,![]() 剪开,拼成如图
剪开,拼成如图![]() 所示的四边形
所示的四边形![]() ,若中间空白部分四边形恰好是正方形
,若中间空白部分四边形恰好是正方形![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,则正方形的面积是( )
,则正方形的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
首先设设正方形的边长为a,长方形的长为b,宽为c,则MP=MQ+QP=NQ-RQ,即a=c+QP=b-RQ,得出QP=a-c,RQ=b-a,再根据QP=RQ,即a-c=b-a,得出2a=b+c,进而得出平行四边形的面积为![]() =72,解得a=6,b=12,即可得解.
=72,解得a=6,b=12,即可得解.
由题意可知,设正方形的边长为a,长方形的长为b,宽为c
则MP=MQ+QP=NQ-RQ,即a=c+QP=b-RQ
∴QP=a-c,RQ=b-a
又QP=RQ,即a-c=b-a
∴2a=b+c
∴平行四边形的面积为![]() =72
=72
∴a=6,b=12
∴RQ=12-6=6
∴正方形的面积是36
故答案为C.

练习册系列答案
相关题目