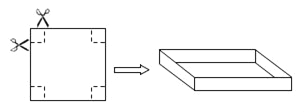
题目内容
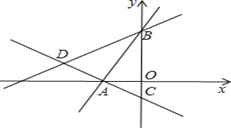
【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
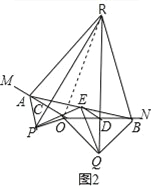
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小.

【答案】(1)证明见解析;
(2)证明见解析;
(3)∠MON=135°.
【解析】解(1)证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC=![]() AO=OC=ED,CE=OD=
AO=OC=ED,CE=OD=![]() OB=DQ,
OB=DQ,
在△PCE与△EDQ中,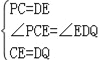 ,
,
∴△PCE≌△EDQ;
(2)如图2,连接RO,
∵PR与QR分别是OA,OB的垂直平分线,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
(3)由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,∵△ARB∽△PEQ,∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD=![]() ∠ARB=45°,
∠ARB=45°,
∴∠MON=135°,

练习册系列答案
相关题目