��Ŀ����
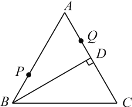
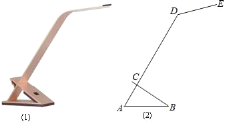
����Ŀ����ͼ��1����һ�ּ���̨�ƣ�����ṹͼ��2���е���Ϊ��ABC��BC������ֲ��ƣ���A��C��D��ͬһֱ���ϣ����á�ACB=90�㣬��A=60�㣬AB=16cm����ADE=135�㣬�Ƹ�CD��Ϊ40cm���ƹ�DE��Ϊ15cm��
��1����DE��ˮƽ���棨AB����ֱ�ߣ����ɵĽǣ�
��2����̨�Ƶĸߣ���E������ľ��룬�����ȷ��0.1cm����
���ο����ݣ�sin15��=0.26��cos15��=0.97��tan15��=0.27��sin30��=0.5��cos30��=0.87��tan30��=0.58����
���𰸡���1��15�㣻��2��45.5cm��
��������
��1��ֱ������ƽ���ߺʹ��߽����ó���EDF��ֵ��
��2������������Ǻ�����ϵ�ó�DN�Լ�EF��ֵ�������ó��𰸣�
��1����ͼ��ʾ������D��DF��AB������D��DN��AB�ڵ�N��EF��AB�ڵ�M��
������ɵã��ı���DNMF�Ǿ��Σ�
���NDF=90�㣬
�ߡ�A=60�㣬��AND=90�㣬
���ADN=30�㣬
���EDF=135�㩁90�㩁30��=15�㣬
��DE��ˮƽ���棨AB����ֱ�ߣ����ɵĽ�Ϊ15�㣻
��2����ͼ��ʾ���ߡ�ACB=90�㣬��A=60�㣬AB=16cm��
���ABC=30�㣬��AC=![]() AB=8cm��
AB=8cm��
�ߵƸ�CD��Ϊ40cm��
��AD=48cm��
��DN=ADsin60��=24![]() cm��
cm��
��FM=24![]() cm��
cm��
�ߵƹ�DE��Ϊ15cm��
��sin15��=![]() =
=![]() =0.26��
=0.26��
��ã�EF=3.9��
��̨�Ƶĸ�Ϊ��3.9+24![]() ��45.5��cm����
��45.5��cm����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�