题目内容
【题目】如图，直线
与
轴交于点
，与
轴交于点
，抛物线
经过、两点．
求抛物线的解析式；
如图，点
是直线
上方抛物线上的一动点，当
面积最大时，请求出点的坐标和面积的最大值？
在的结论下，过点作轴的平行线交直线于点
，连接
，点
是抛物线对称轴上的动点，在抛物线上是否存在点
，使得以、、
、为顶点的四边形是平行四边形？如果存在，请直接写出点的坐标；如果不存在，请说明理由．
【答案】（1）
；（2）当
时，即点
的坐标是
时，
的面积最大，最大面积是
；（3）点
的坐标是
、
、
．
【解析】
（1）首先根据直线y=﹣
x+3与x轴交于点C，与y轴交于点B，求出点B的坐标是（0，3），点C的坐标是（4，0）；然后根据抛物线y=ax2+x+c经过B、C两点，求出a\c的值是多少，即可求出抛物线的解析式．
（2）首先过点E作y轴的平行线EF交直线BC于点M，EF交x轴于点F，然后设点E的坐标是（x，﹣
x2+x+3），则点M的坐标是（x，﹣x+3），求出EM的值是多少；最后根据三角形的面积的求法，求出S△ABC，进而判断出当△BEC面积最大时，点E的坐标和△BEC面积的最大值各是多少即可．
（3）在抛物线上存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形．然后分三种情况讨论，根据平行四边形的特征，求出使得以P、Q、A、M为顶点的四边形是平行四边形的点P的坐标是多少即可．
（1）∵直线y=﹣x+3与x轴交于点C，与y轴交于点B，∴点B的坐标是（0，3），点C的坐标是（4，0）．
∵抛物线y=ax2+x+c经过B、C两点，∴
，解得：
，∴y=﹣x2+x+3．
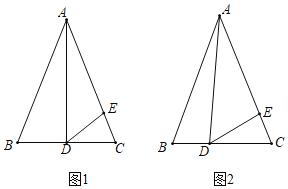
（2）如图1，过点E作y轴的平行线EF交直线BC于点M，EF交x轴于点F．
∵点E是直线BC上方抛物线上的一动点，∴设点E的坐标是（x，﹣x2+x+3），则点M的坐标是（x，﹣x+3），∴EM=﹣x2+x+3﹣（﹣x+3）=﹣x2+
x，∴S△BEC=S△BEM+S△MEC
=
=
×（﹣x2+x）×4=﹣x2+3x=﹣（x﹣2）2+3
∴当x=2时，即点E的坐标是（2，3）时，△BEC的面积最大，最大面积是3．
（3）在抛物线上存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形．
①如图2，由（2），可得点M的横坐标是2．
∵点M在直线y=﹣x+3上，∴点M的坐标是（2，）．
又∵点A的坐标是（﹣2，0），∴AM=
=
，∴AM所在的直线的斜率是：
；
∵y=﹣x2+x+3的对称轴是x=1，∴设点Q的坐标是（1，m），点P的坐标是（x，﹣x2+x+3），则
解得：
或
．
∵x＜0，∴点P的坐标是（﹣3，﹣
）．
②如图3，由（2），可得点M的横坐标是2．
∵点M在直线y=﹣x+3上，∴点M的坐标是（2，）．
又∵点A的坐标是（﹣2，0），∴AM==，∴AM所在的直线的斜率是：；
∵y=﹣x2+x+3的对称轴是x=1，∴设点Q的坐标是（1，m），点P的坐标是（x，﹣x2+x+3），则
解得：或．
∵x＞0，∴点P的坐标是（5，﹣）．
③如图4，由（2），可得点M的横坐标是2．
∵点M在直线y=﹣x+3上，∴点M的坐标是（2，）．
又∵点A的坐标是（﹣2，0），∴AM==．
∵y=﹣x2+x+3的对称轴是x=1，∴设点Q的坐标是（1，m），点P的坐标是（x，﹣x2+x+3），则
，解得：
，∴点P的坐标是（﹣1，
）．
综上，可得在抛物线上存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形，点P的坐标是（﹣3，﹣）、（5，﹣）、（﹣1，）．
