Question

【题目】定义：若△ABC中，其中一个内角是另一个内角的一半，则称△ABC为“半角三角形”．

（1）若Rt△ABC为半角三角形，∠A=90°，则其余两个角的度数为．

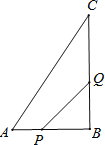
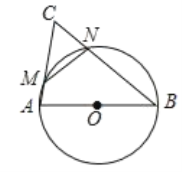
（2）如图，以△ABC的边AB为直径画圆，与边AC交于M，与边BC交于N，已知CN=AC

①求证：∠C=60°．

②若△ABC是半角三角形，求∠B的度数．

Answer 1

【答案】（1）45°，45°或30°，60°；（2）略；（3）30°，40°，80°，90°

【解析】

（1）根据“半角三角形”的定义即可解决问题；

（2）①只要证明△CMN∽△CBA，可得，即，在Rt△ACN中，sin∠，即可推出∠CAN＝30°解决问题；

②根据“半角三角形”的定义即可解决问题.

(1)∵Rt△ABC为半角三角形，∠A＝90°，

∴∠B＝∠C＝45°，或∠B＝60°，∠C＝30°或∠B＝30°，∠C＝60°，

∴其余两个角的度数为45°，45°或30°，60°，

故答案为45°，45°或30°，60°．

(2)①如图中，连接AN．

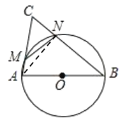
∵AB是直径，

∴∠ANB＝90°，

∵∠C＝∠C，∠CMN＝∠B，

∴△CMN∽△CBA，

∴，即，

在Rt△ACN中，sin∠CAN＝，

∴∠CAN＝30°，

∴∠C＝60°．

②∵△ABC是半角三角形，∠C＝60°，

所以如果∠B是△ABC中∠C的一半，则∠B＝30°.

如果∠A是△ABC中∠C的一半，则∠A＝30°，故∠B＝90°.

如果∠B是△ABC中∠A的一半，则∠B＝，故∠B＝40°.

如果∠A是△ABC中∠B的一半，则∠B＝，故∠B＝80°.

∴∠B＝30°或40°或80°或90°．