题目内容
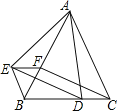
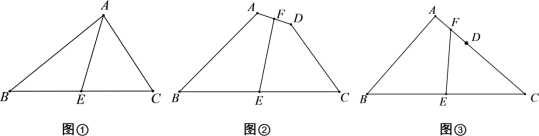
【题目】(发现问题)爱好数学的小强在做作业时碰到这样的一道题目:如图①,在△ABC中,AB=8,AC=6,E为BC中点,求AE的取值范围.
(解决问题)
(1)小强经过多次的尝试与探索,终于得到解题思路:在图①中,作AB边上的中点F,连接EF,构造出△ABC的中位线EF,请你完成余下的求解过程.
(灵活运用)
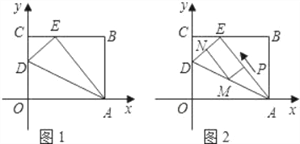
(2)如图②,在四边形ABCD中,AB=8,CD=6,E、F分别为BC、AD中点,求EF的取值范围.
(3)变式:把图②中的A、D、C变成在一直线上时,如图③,其它条件不变,则EF的取值范围为 .
(迁移拓展)
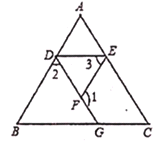
(4)如图④,在△ABC中,∠A=60°,AB=4,E为BC边的中点,F是AC边上一点且EF正好平分△ABC的周长,则EF= .

【答案】(1)详见解析;(2)1<EF<7;(3)![]() ;(4)EF=
;(4)EF=![]() .
.
【解析】
(1)依照题意作出图形,利用△AFE中两边之和大于第三边,两边之差小于第三边,求解AE边的取值范围;
(2)连接BD,取BD 中点G,连接FG、EG,由E、F分别为BC、AD中点,可得FG=![]() AB,EG=
AB,EG=![]() DC,同(1)△GEF中两边之和大于第三边,两边之差小于第三边,求解EF边的取值范围;
DC,同(1)△GEF中两边之和大于第三边,两边之差小于第三边,求解EF边的取值范围;
(3)如图,连接BD,取BD的中点H,连接HF,HE,由三角形中位线定理可知![]() ,
,![]() ,在△DHE中有,两边之和大于第三边,两边之差小于第三边,即可求得
,在△DHE中有,两边之和大于第三边,两边之差小于第三边,即可求得![]() ;
;
(4)在线段CF上取一点M,使得FM=AF,连接BM,取BM的中点N,连接FN,EN,由EF平分三角形ABC周长,可得CM=AB=4,由三角形中位线定理,及∠A=60°,可知NF=NE=2,且∠FNE=120°,作NO⊥EF于O,解△ENF,可得FO=E0=![]() ,即可求得EF=
,即可求得EF=![]() .
.
(1)解:
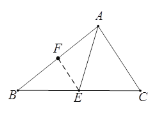
∵E 为 BC 中点,F为 AB 中点,
∴EF=![]() AC,
AC,
∵AB=8,AC=6,
∴AF=![]() AB=4,EF=
AB=4,EF=![]() AC=3,
AC=3,
在△AEF中,两边之和大于第三边,两边之差小于第三边,
∴4-3<AE<4+3,
即,1<AE<7;
(2)解:连接BD,取BD 中点G,连接FG、EG,

∵E、F分别为BC、AD中点,
∴FG=![]() AB,EG=
AB,EG=![]() DC,
DC,
∵AB=8,CD=6,
∴FG=4,EG=3,
在△GEF中,4-3<EF<4+3,
即1<EF<7.
(3)如图,连接BD,取BD的中点H,连接HF,HE,

∵E、F分别为BC、AD中点,
∴![]() ,
,![]()
∴在△DHE中,![]() ,
,
即EF的取值范围为![]() ,
,
故答案为:![]() ;
;
(4)在线段CF上取一点M,使得FM=AF,连接BM,取BM的中点N,连接FN,EN,
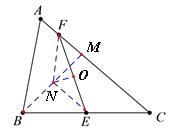
∴F为线段AM的中点,
∵E为BC中点,
∴FN∥AB,且![]() ,EN∥AC,且
,EN∥AC,且![]() ,BE=EC,
,BE=EC,
∵∠A=60°,AB=4,
∴FN=2,∠FNE=120°,
∵EF正好平分△ABC的周长,
∴![]() ,
,
∴![]() ,
,
∴CM=4,
∴NE=2,
∴△FNE为等腰三角形,且∠NFE=∠NEF=30°,
过点N作NO⊥EF于点O,
则FO=OE=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.