题目内容
已知|x+y+1|+(x-y+3)2=0,则(x+y)2004等于
- A.22004
- B.-1
- C.1
- D.-22004
C
分析:先根据非负数的和等于0,则每一项都等于0列出方程组,再根据x的系数相等,y的系数互为相反数,利用加减消元法即可求出x、y的值,然后代入计算即可.
解答:根据题意得,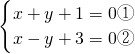 ,
,
①+②得,2x+4=0,
解得x=-2,
①-②得,2y-2=0,
解得y=1,
∴方程组的解是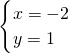 ,
,
∴(x+y)2004=(-2+1)2004=(-1)2004=1.
故选C.
点评:本题考查了非负数的性质及二元一次方程组的解法,系数的特点是决定选择利用加减消元法还是利用代入消元法的关键.
分析:先根据非负数的和等于0,则每一项都等于0列出方程组,再根据x的系数相等,y的系数互为相反数,利用加减消元法即可求出x、y的值,然后代入计算即可.
解答:根据题意得,
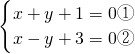 ,
,①+②得,2x+4=0,
解得x=-2,
①-②得,2y-2=0,
解得y=1,
∴方程组的解是
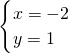 ,
,∴(x+y)2004=(-2+1)2004=(-1)2004=1.
故选C.
点评:本题考查了非负数的性质及二元一次方程组的解法,系数的特点是决定选择利用加减消元法还是利用代入消元法的关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
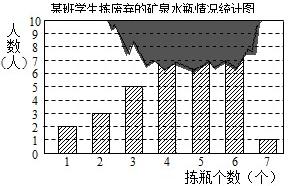 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.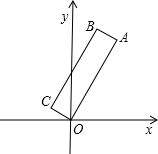 如图,已知矩形ABCD,OA与x轴正半轴夹角为60°,点A的横坐标为2,点C的横坐标为
如图,已知矩形ABCD,OA与x轴正半轴夹角为60°,点A的横坐标为2,点C的横坐标为