题目内容
在学习三角形中线的知识时,小明了解到:三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。进而,小明继续研究,过四边形的某一顶点的直线能否将该四边形平分为面积相等的两部分?他画出了如下示意图(如图1),得到了符合要求的直线AF.


小明的作图步骤如下:
第一步:连结AC;
第二步:过点B作BE//AC交DC的延长线于点E;
第三步:取ED中点F,作直线AF;
则直线AF即为所求.
请参考小明思考问题的方法,解决问题:
如图2,五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C(4,0),D(4,2).请你构造一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,并求出该直线的解析式.


小明的作图步骤如下:
第一步:连结AC;
第二步:过点B作BE//AC交DC的延长线于点E;
第三步:取ED中点F,作直线AF;
则直线AF即为所求.
请参考小明思考问题的方法,解决问题:
如图2,五边形ABOCD,各顶点坐标为:A(3,4),B(0,2),O(0,0),C(4,0),D(4,2).请你构造一条经过顶点A的直线,将五边形ABOCD分为面积相等的两部分,并求出该直线的解析式.
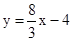 .
.试题分析:如图,构造图形:连结AO,作BM∥AO交x轴于点M;连结AC,作DN∥AC交x轴于点N;取MN的中点F,作AH⊥x轴于点H.通过△BMO∽△AOH的对应边成比例得到:
 ,则易求MO=1.5.同理CN=0.5.所以M(-1.5,0),N(4.5,0),则MN的中点F(1.5,0).设直线AF的解析式为:y=kx+b(k≠0).把点A(3,4),F(1.5,0)的坐标分别代入,列出关于k、b的方程组,通过解方程组来求系数k、b的值.
,则易求MO=1.5.同理CN=0.5.所以M(-1.5,0),N(4.5,0),则MN的中点F(1.5,0).设直线AF的解析式为:y=kx+b(k≠0).把点A(3,4),F(1.5,0)的坐标分别代入,列出关于k、b的方程组,通过解方程组来求系数k、b的值.如图,连结AO,作BM∥AO交x轴于点M;连结AC,作DN∥AC交x轴于点N;取MN的中点F,作AH⊥x轴于点H.
∵BM∥AO,
∴∠BMO=∠AOH.
∵∠BOM=∠AHO=90°,
∴△BMO∽△AOH,
∴
 ,即
,即 ,解得,MO=1.5.
,解得,MO=1.5.同理 CN=0.5.
∴M(-1.5,0),N(4.5,0),
∴MN的中点F(1.5,0).
设直线AF的解析式为:y=kx+b(k≠0).
把点A(3,4),F(1.5,0)的坐标代入,得
 ,解得
,解得 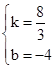 .
.∴直线AF的解析式为:
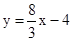 .
.
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
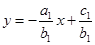 与
与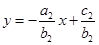 的交点为
的交点为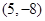 ,则方程组
,则方程组 的解为 。
的解为 。 满足不等式组
满足不等式组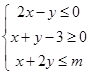 ,且
,且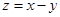 的最小值为
的最小值为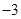 ,则实数
,则实数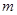 的值是 .
的值是 .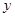 (千米)与时间
(千米)与时间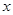 (小时)的函数关系的大致图象是( )
(小时)的函数关系的大致图象是( )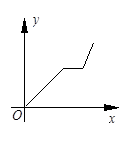
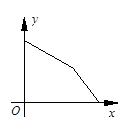
 集,甲、乙两部连续剧的收视观众的人次的总和为
集,甲、乙两部连续剧的收视观众的人次的总和为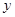 万人次,求
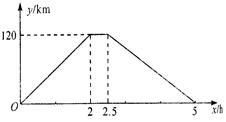
万人次,求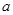 千米,休息了一段时间,又原路原速返回了
千米,休息了一段时间,又原路原速返回了 千米(
千米(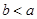 ),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离
),再掉头沿原方向以比原速大的速度行驶,则此人离起点的距离 与时间
与时间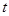 的函数关系的大致图象是( ).
的函数关系的大致图象是( ).