题目内容
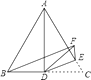
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AE是经过A点的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,CE=2,BD=6,则DE的长为.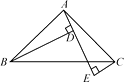
【答案】4
【解析】∵BD⊥AE,
∴∠BDA=90°,
∴∠ABD+∠BAD=90°,
又∠BAC=90°,
∴∠CAD+∠BAD=90°,
∴∠ABD=∠CAD,
在△ABD和△CAE中,
∴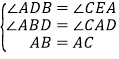 ,
,
∴△ABD≌△CAE,
又∵CE=2,BD=6,
∴BD=AE=6,AD=CE=2,
∴DE=AE-AD=BD-CE=6-2=4.
所以答案是:4.
【考点精析】根据题目的已知条件,利用余角和补角的特征的相关知识可以得到问题的答案,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目