题目内容
(本题满分10分)
已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
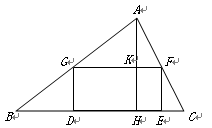
已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.

解:设EF=x,则GF=2x.
∵GF∥BC,AH⊥BC,∴AK⊥GF.
∵GF∥BC,∴△AGF∽△ABC.………………………………………(2分)
∴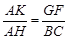 .……………………………………………………………(2分)
.……………………………………………………………(2分)
∵AH=6,BC=12,∴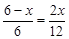 .………………………………………(2分)
.………………………………………(2分)
解得x=3.…………………………………………………………………(2分)
∴矩形DEFG的周长为18.
∵GF∥BC,AH⊥BC,∴AK⊥GF.
∵GF∥BC,∴△AGF∽△ABC.………………………………………(2分)
∴
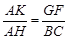 .……………………………………………………………(2分)
.……………………………………………………………(2分)∵AH=6,BC=12,∴
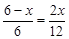 .………………………………………(2分)
.………………………………………(2分)解得x=3.…………………………………………………………………(2分)
∴矩形DEFG的周长为18.
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
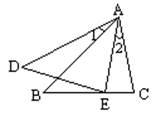
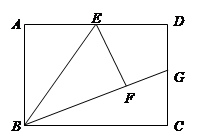
 (3)是否存在这样的点P,使△CDP的周长等于△PAE周长的2倍?若存在,求DP的长;若不存在,请说明理由.
(3)是否存在这样的点P,使△CDP的周长等于△PAE周长的2倍?若存在,求DP的长;若不存在,请说明理由.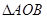 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在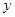 轴和
轴和 轴上,
轴上, ∠ABO=
∠ABO=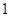 .
.
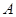 作
作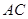 ∥
∥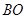 交上述函数图像于点
交上述函数图像于点 ,点
,点 在上述函数图像上,当
在上述函数图像上,当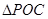 与
与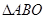 相似时,求点
相似时,求点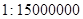 的卫星地图上,测得上海和南京的距离大约是
的卫星地图上,测得上海和南京的距离大约是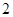 厘米.那么上海和南京的实际距离大约是 ▲ 千米.
厘米.那么上海和南京的实际距离大约是 ▲ 千米.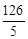 ;
;

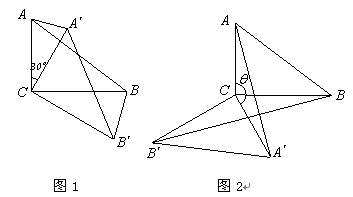
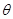 (0°<
(0°<