题目内容
已知在平面直角坐标系中，四边形OABC是矩形，点A、C的坐标分别为A（3，0）、C（0，4），点D的坐标为D（-5，0），点P是直线AC上的一动点，直线DP与y轴交于点M．问：（1）当点P运动到何位置时，直线DP平分矩形OABC的面积，请简要说明理由，并求出此时直线DP的函数解析式；
（2）当点P沿直线AC移动时，是否存在使△DOM与△ABC相似的点M，若存在，请求出点M的坐标；若不存在，请说明理由；
（3）当点P沿直线AC移动时，以点P为圆心、半径长为R（R＞0）画圆，所得到的圆称为动圆P．若设动圆P的直径长为AC，过点D作动圆P的两条切线，切点分别为点E、F．请探求是否存在四边形DEPF的最小面积S，若存在，请求出S的值；若不存在，请说明理由．注：第（3）问请用备用图解答．
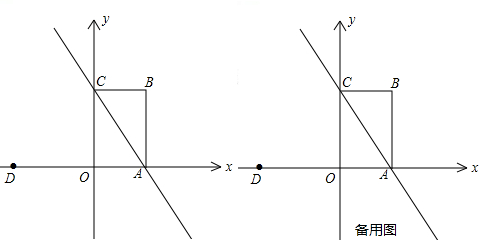
分析：（1）根据矩形的性质（经过矩形中心的直线把矩形分成面积相等的两个部分）可知，连接BO与AC交于点H，则当点P运动到点H时，直线DP平分矩形OABC的面积．先求出点P的坐标为P（
，2），结合点D坐标利用待定系数法求直线DP的函数解析式为：y=
x+
．
（2）根据题意可知存在点M使得△DOM与△ABC相似，设直线DP与y轴的正半轴交于点M（0，ym）．可利用相似中的相似比分别列出关于点M的坐标有关的方程，求解即可．注意：共有3种情况，要考虑周全．
（3）过D作DP⊥AC于点P，以P为圆心，半径长为
画圆，过点D分别作⊙P的切线DE、DF，点E、F是切点．除P点外在直线AC上任取一点P1，半径长为
画圆，过点D分别作⊙P的切线DE1、DF1，点E1、F1是切点．在△DEP和△DFP中，△DPE≌△DPF．所以S四边形DEPF=2S△DPE=
DE．可知当DE取最小值时，S四边形DEPF的值最小．所以当DE是D点与切点所连线段长的最小值．利用相似求得DE的长，再求得S四边形DEPF=
．
| 3 |
| 2 |
| 4 |
| 13 |
| 20 |
| 13 |
（2）根据题意可知存在点M使得△DOM与△ABC相似，设直线DP与y轴的正半轴交于点M（0，ym）．可利用相似中的相似比分别列出关于点M的坐标有关的方程，求解即可．注意：共有3种情况，要考虑周全．
（3）过D作DP⊥AC于点P，以P为圆心，半径长为
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| ||
| 4 |
解答：解：（1）连接BO与AC交于点H，则当点P运动到点H时，直线DP平分矩形OABC的面积．理由如下：
∵矩形是中心对称图形，且点H为矩形的对称中心．
又据经过中心对称图形对称中心的任一直线平分此中心对称图形的面积，
因为直线DP过矩形OABC的对称中心点H，所以直线DP平分矩形OABC的面积．（2分）
由已知可得此时点P的坐标为P（
，2）．
设直线DP的函数解析式为y=kx+b．
则有
，解得k=
，b=
．
所以，直线DP的函数解析式为：y=
x+
．（5分）
（2）存在点M使得△DOM与△ABC相似．
如图，不妨设直线DP与y轴的正半轴交于点M（0，ym）．
因为∠DOM=∠ABC，若△DOM与△ABC相似，则有
=
或
=
．
当
=
时，即
=
，解得ym=
．所以点M1（0，
）满足条件．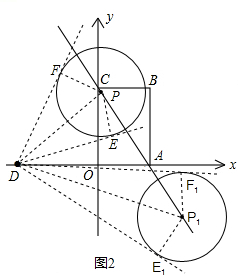
当
=
时，即
=
，解得ym=
．所以点M2（0，
）满足条件．
由对称性知，点M3（0，-
）也满足条件．
综上所述，满足使△DOM与△ABC相似的点M有3个，
分别为M1（0，
）、M2（0，
）、M3（0，-
）．
（3）如图，过D作DP⊥AC于点P，以P为圆心，半径长为
画圆，
过点D分别作⊙P的切线DE、DF，点E、F是切点．除P点外在直线AC上任取一点P1，半径长为
画圆，
过点D分别作⊙P的切线DE1、DF1，点E1、F1是切点．
在△DEP和△DFP中，∠PED=∠PFD，PF=PE，PD=PD，
∴Rt△DPE≌Rt△DPF．
∴S四边形DEPF=2S△DPE=2×
×DE•PE=DE•PE=
DE．
∴当DE取最小值时，S四边形DEPF的值最小．
∵DE2=DP2-PE2，DE12=DP12-P1E12，
∴DE12-DE2=DP12-DP2．
∵DP1＞DP，∴DE12-DE2＞0．
∴DE1＞DE．由P1点的任意性知：DE是D点与切点所连线段长的最小值．（12分）
在△ADP与△AOC中，∠DPA=∠AOC，
∠DAP=∠CAO，∴△ADP∽△ACO．
∴
=
，即
=
．
∴DP=
．
∴DE=
=
=
．
∴S四边形DEPF=
，即S=
．（14分）
（注：本卷中所有题目，若由其它方法得出正确结论，请参照标准给分．）
∵矩形是中心对称图形，且点H为矩形的对称中心．
又据经过中心对称图形对称中心的任一直线平分此中心对称图形的面积，
因为直线DP过矩形OABC的对称中心点H，所以直线DP平分矩形OABC的面积．（2分）
由已知可得此时点P的坐标为P（
| 3 |
| 2 |
设直线DP的函数解析式为y=kx+b．
则有
|
| 4 |
| 13 |
| 20 |
| 13 |
所以，直线DP的函数解析式为：y=
| 4 |
| 13 |
| 20 |
| 13 |
（2）存在点M使得△DOM与△ABC相似．
如图，不妨设直线DP与y轴的正半轴交于点M（0，ym）．
因为∠DOM=∠ABC，若△DOM与△ABC相似，则有
| OM |
| OD |
| BC |
| AB |
| OM |
| OD |
| AB |
| BC |
当
| OM |
| OD |
| BC |
| AB |
| ym |
| 5 |
| 3 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
当
| OM |
| OD |
| AB |
| BC |
| ym |
| 5 |
| 4 |
| 3 |
| 20 |
| 3 |
| 20 |
| 3 |
由对称性知，点M3（0，-
| 15 |
| 4 |
综上所述，满足使△DOM与△ABC相似的点M有3个，
分别为M1（0，
| 15 |
| 4 |
| 20 |
| 3 |
| 15 |
| 4 |
（3）如图，过D作DP⊥AC于点P，以P为圆心，半径长为
| 5 |
| 2 |
过点D分别作⊙P的切线DE、DF，点E、F是切点．除P点外在直线AC上任取一点P1，半径长为
| 5 |
| 2 |
过点D分别作⊙P的切线DE1、DF1，点E1、F1是切点．
在△DEP和△DFP中，∠PED=∠PFD，PF=PE，PD=PD，
∴Rt△DPE≌Rt△DPF．
∴S四边形DEPF=2S△DPE=2×
| 1 |
| 2 |
| 5 |
| 2 |
∴当DE取最小值时，S四边形DEPF的值最小．
∵DE2=DP2-PE2，DE12=DP12-P1E12，
∴DE12-DE2=DP12-DP2．
∵DP1＞DP，∴DE12-DE2＞0．
∴DE1＞DE．由P1点的任意性知：DE是D点与切点所连线段长的最小值．（12分）
在△ADP与△AOC中，∠DPA=∠AOC，
∠DAP=∠CAO，∴△ADP∽△ACO．
∴
| DP |
| DA |
| CO |
| CA |
| DP |
| 8 |
| 4 |
| 5 |
∴DP=
| 32 |
| 5 |
∴DE=
| DP2-PE2 |
|
| ||
| 10 |
∴S四边形DEPF=
| ||
| 4 |
| ||
| 4 |
（注：本卷中所有题目，若由其它方法得出正确结论，请参照标准给分．）
点评：主要考查了一次函数和几何图形的综合运用．解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度，再结合具体图形的性质求解．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
已知在平面直角坐标系xOy中，⊙O的半径为1．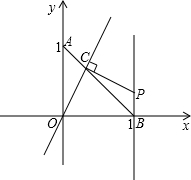
直线交线段AB于点C，过点C作OC的垂线与直线x=1相交于点P，设AC=t，点P的坐标为（1，y），
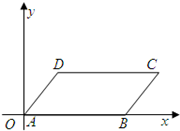如图，已知在平面直角坐标系中，平行四边形ABCD顶点A（0，0），C（10，4），直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分，求a的值．