题目内容
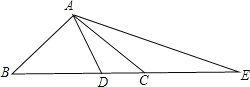
【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
【答案】(1)450;(2)不改变;(3)∠DAE=![]() ∠BAC.
∠BAC.
【解析】
(1)要求∠DAE,必先求∠BAD和∠CAE,由∠BAC=90°,AB=AC,可求∠B=∠ACB=45°,又因为BD=BA,可求∠BAD=∠BDA=67.5°,再由CE=CA,可求∠CAE=∠E=22.5°,所以∠DAE=∠BAE-∠BAD=112.5°-67.5°=45°;
(2)先设∠CAE=x,由已知CA=CE可求∠ACB=∠CAE+∠E=2x,∠B=90°-2x,又因为BD=BA,所以∠BAD=∠BDA=x+45°,再根据三角形的内角和是180°,可求∠BAE=90°+x,即∠DAE=∠BAE-∠BAD=(90°+x)-(x+45°)=45度;
(3)可设∠CAE=x,∠BAD=y,则∠B=180°-2y,∠E=∠CAE=x,所以∠BAE=180°-∠B-∠E=2y-x,∠BAC=∠BAE-∠CAE=2y-x-x=2y-2x,即∠DAE=![]() ∠BAC.
∠BAC.
(1)∵AB=AC,∠BAC=![]() ,
,
∴∠B=∠ACB=![]() ,
,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180∠B)=
(180∠B)=![]()
∵CE=CA,
∴∠CAE=∠E=![]() ∠ACB=
∠ACB=![]() ,
,
在△ABE中,∠BAE=180∠B∠E=![]() ,
,
∴∠DAE=∠BAE∠BAD=![]()
![]() =
=![]() ;
;
(2)不改变.
设∠CAE=x,
∵CA=CE,
∴∠E=∠CAE=x,
∴∠ACB=∠CAE+∠E=2x,
在△ABC中,∠BAC=![]() ,
,
∴∠B=![]() ∠ACB=
∠ACB=![]() 2x,
2x,
∵BD=BA,
∴∠BAD=∠BDA=![]() (180∠B)=x+
(180∠B)=x+![]() ,
,
在△ABE中,∠BAE=![]() ∠B∠E,=
∠B∠E,=![]() (
(![]() 2x)x=
2x)x=![]() +x,
+x,
∴∠DAE=∠BAE∠BAD,=(![]() +x)(x+
+x)(x+![]() )=
)=![]() ;
;
(3)∠DAE=![]() ∠BAC.
∠BAC.
理由:设∠CAE=x,∠BAD=y,
则∠B=![]() 2y,∠E=∠CAE=x,
2y,∠E=∠CAE=x,
∴∠BAE=![]() ∠B∠E=2yx,
∠B∠E=2yx,
∴∠DAE=∠BAE∠BAD=2yxy=yx,
∠BAC=∠BAE∠CAE=2yxx=2y2x,
∴∠DAE=![]() ∠BAC.
∠BAC.

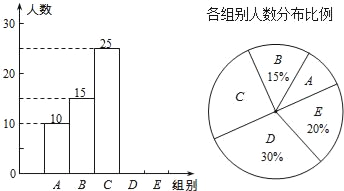
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.