Question

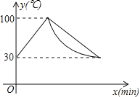
【题目】如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：

①∠AOB＝90°+∠C；

②AE+BF＝EF；

③当∠C＝90°时，E，F分别是AC，BC的中点；

④若OD＝a，CE+CF＝2b，则S△CEF＝ab．

其中正确的是（　　）

A.①②B.③④C.①②④D.①③④

Answer 1

【答案】C

【解析】

根据角平分线的定义和三角形内角和定理判断①；根据角平分线的定义和平行线的性质判断②；根据三角形三边关系判断③；根据角平分线的性质判断④．

∵∠BAC和∠ABC的平分线相交于点O，

∴∠OBA＝∠CBA，∠OAB＝∠CAB，

∴∠AOB＝180°﹣∠OBA﹣∠OAB

＝180°﹣∠CBA﹣∠CAB

＝180°﹣（180°﹣∠C）

＝90°+∠C，①正确；

∵EF∥AB，

∴∠FOB＝∠ABO，又∠ABO＝∠FBO，

∴∠FOB＝∠FBO，

∴FO＝FB，

同理EO＝EA，

∴AE+BF＝EF，②正确；

当∠C＝90°时，AE+BF＝EF＜CF+CE，

∴E，F不是AC，BC的中点，③错误；

作OH⊥AC于H，

∵∠BAC和∠ABC的平分线相交于点O，

∴点O在∠C的平分线上，

∴OD＝OH，

∴S△CEF＝×CF×OD×CE×OH＝ab，④正确．

故选：C．