题目内容
【题目】下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( ) 
A.160
B.161
C.162
D.163
【答案】B
【解析】方法一: 解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
故选B.
方法二:![]() ,
, ![]() ,
, ![]() ,
, 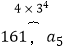 ,…
,… 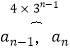 ,
,
∴  ,
,
(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(an﹣an﹣1)=an﹣a1 ,
∴an﹣a1=4×(3+32+…+3n﹣1)=4×(3+32+…+3n﹣1)= ![]() (用错位相减法可求出)
(用错位相减法可求出)
∴ ![]() ,
,
∵a1=5,
∴ ![]() .
.
由图可以看出:第一个图形中由角上的3个三角形加上中间1个小三角形再加上外围1个大三角形共有5个正三角形;下一个图形的三个角上的部分是上一个图形的全部,另外加上中间一个小的三角形和外围的一个大三角形,所以第二个图形中有5×3+1+1=17个正三角形,第三个图形中有17×3+1+1=53个正三角形,第四个图形中有53×3+1+1=161个正三角形.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目