题目内容
【题目】如图,在RtΔABC中,∠C=90, BC=6cm, AC=8cm,如果按图中所示方法将ΔBCD沿BD折叠,使点C落在边AB上的点C'处,那么ΔADC'的周长是________cm.

【答案】12.
【解析】
先根据勾股定理得到AB=10cm,再根据折叠的性质得到DC=DC′,BC=BC′=6cm,则AC′=4cm,然后可求出ΔADC'的周长.
解: 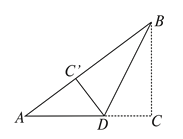 ,
,
∵∠C=90°,BC=6cm,AC=8cm,
∴AB=![]() =10cm,
=10cm,
∵将△BCD沿BD折叠,使点C落在AB边的C′点,
∴△BCD≌△BC′D,
∴DC=DC′,BC=BC′=6cm,
AC′=AB- BC′=10-6=4
ΔADC'的周长= AC′+ DC′+AD=4+DC+AD=4+AC=4+8=12(cm).
故答案是:12.

练习册系列答案
相关题目