Question

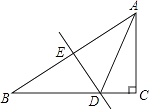
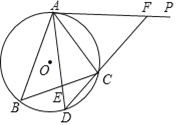
【题目】如图1，⊙O是△ABC的外接圆，AP是⊙O的切线．已知AC=4，BC=5．

（1）求证：∠PAC=∠ABC；

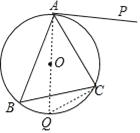
（2）作∠BAC的平分线，与⊙O相交于点D，与BC相交于点E，连接并延长DC，与AP相交于点F（如图2），若AE=AC，求CF的长．

Answer 1

【答案】（1）见解析　　（2）

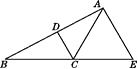
【解析】（1）作直径AQ，连接QC，根据切线的性质得出∠PAQ=90°，求出∠PAC+∠CAQ=90°，根据圆周角定理得出∠ACQ=90°，∠PAC=∠Q，即可求出答案；

（2）求出∠AEC=∠ACE，∠FAC=∠ABC，根据相似三角形的判定得出△FAC∽△ABC，得出比例式，代入求出即可．

（1）证明：

作直径AQ，连接QC，

∵AP是⊙O的切线，

∴∠PAQ=90°，

∴∠PAC+∠CAQ=90°，

∵AQ是直径，

∴∠ACQ=90°，

∴∠CAQ+∠Q=90°，

∴∠PAC=∠Q，

∵∠Q=∠ABC，

∴∠PAC=∠ABC；

（2）解：∵AD是∠BAC的平分线，

∴∠BAD=∠CAD，

∴∠ACF=∠ADC+∠CAD=∠ABC+∠BAD=∠AEC，

∵AE=AC，

∴∠AEC=∠ACE，

由（1）知：∠FAC=∠ABC，

∴△FAC∽△ABC，

∴=，

即=，

∴CF=．