题目内容
【题目】如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为cm.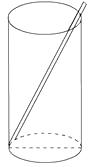
【答案】7
【解析】当杯子如图中所放的方式时,露在杯子外面的长度最小,在杯中的筷子与圆柱形水杯的底面直径和高构成了直角三角形,由勾股定理可求出筷子在水杯中的长度,筷子总长度减去杯子里面的长度即露在外面的长度.设杯子底面直径为a,高为b,筷子在杯中的长度为c,根据勾股定理,得:c2=a2+b2 , 故:c=13,则筷子露在外面最短为20-13=7cm,当杯子如图中所放的方式时,露在杯子外面的长度最小,在杯中的筷子与圆柱形水杯的底面直径和高构成了直角三角形,由勾股定理可求出筷子在水杯中的长度,筷子总长度减去杯子里面的长度即露在外面的长度。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目