Question

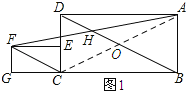
【题目】如图，已知在矩形ABCD中，BC=2CD=2a，点E在边CD上，在矩形ABCD的左侧作矩形ECGF，使CG=2GF=2b，连接BD，CF，连结AF交BD于点H．

（1）求证：BD∥CF；

（2）求证：H是AF的中点；

（3）连结CH，若HC⊥BD，求a：b的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）a：b=．

【解析】

试题分析：（1）由矩形的性质可知∠G=∠DCB=90°，由BC=2CD=2a，CG=2GF=2b，可知，依据两边对应成比例且夹角相等的两个三角形相似可知：△FGC∽△DCB，由相似三角形的性质可知∠FCG=∠DBC，由平行线的判定定理可知：BD∥CF；

（2）如图1所示：连接AC，交BD于点O．由矩形的性质可知：OC=OA，由平行线分线段成比例定理可知HF=AH；

（3）如图2所示：连接CH，CA，AC与BD交于点O．由勾股定理可知：FC=b，AC=a，由矩形的对角线的性质可知DB=AC=a，CO=AC=．由（2）可知HO是△AFC的中位线，由三角形中位线的性质可知：HO=．在△BCD中，利用面积法可求得CH=，最后在△COH中，由勾股定理得到：（）2+（）2=（a）2，从而可求得a：b=．

解：（1）∵四边形ABCD、四边形ECGF均为矩形，

∴∠G=∠DCB=90°．

∵BC=2CD=2a，CG=2GF=2b，

∴．

∴△FGC∽△DCB．

∴∠FCG=∠DBC．

∴BD∥CF．

（2）如图1所示：连接AC，交BD于点O．

∵四边形ABCD为矩形，

∴OC=OA．

又∵FC∥BD，

∴HF=AH．

∴点H是AF的中点．

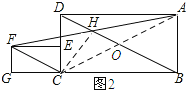
（3）如图2所示：连接CH，CA，AC与BD交于点O．

由勾股定理可知：FC==b，AC==a．

∵四边形ABCD为矩形，

∴DB=AC=a，CO=AC=．

∵HO是△AFC的中位线，

∴HO=FC=．

∵，

∴CH==．

在△COH中，由勾股定理可知：HO2+CH2=OC2，即（）2+（）2=（a）2．

整理得：a2=．

∴a：b=．