题目内容
已知关于 的方程
的方程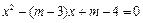 .
.
(1)求证:方程总有两个实数根;
(2)若方程有一个根大于4且小于8,求m的取值范围;
(3)设抛物线
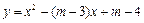 与
与 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求 的值.
的值.
证明:(1)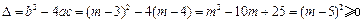 ,
,
所以方程总有两个实数根. ……………………………2分
解:(2)由(1)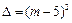 ,根据求根公式可知,
,根据求根公式可知,
方程的两根为: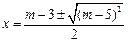
即: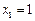 ,
, ,
,
由题意,有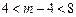 ,即
,即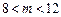 .…………………………5分
.…………………………5分
(3)易知,抛物线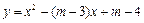 与y轴交点为M(0,
与y轴交点为M(0,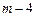 ),由(2)可知抛物线与x轴的
),由(2)可知抛物线与x轴的
交点为(1,0)和(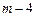 ,0),它们关于直线
,0),它们关于直线 的对称点分别为(0,
的对称点分别为(0, )和(0,
)和(0, 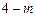 ),
),
由题意,可得:
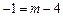 或
或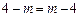 ,即
,即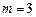 或
或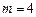 .……………………7分解析:
.……………………7分解析:
略
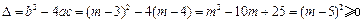 ,
,所以方程总有两个实数根. ……………………………2分
解:(2)由(1)
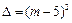 ,根据求根公式可知,
,根据求根公式可知,方程的两根为:
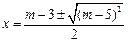
即:
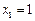 ,
, ,
,由题意,有
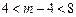 ,即
,即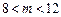 .…………………………5分
.…………………………5分(3)易知,抛物线
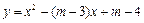 与y轴交点为M(0,
与y轴交点为M(0,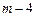 ),由(2)可知抛物线与x轴的
),由(2)可知抛物线与x轴的交点为(1,0)和(
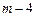 ,0),它们关于直线
,0),它们关于直线 的对称点分别为(0,
的对称点分别为(0, )和(0,
)和(0, 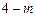 ),
),由题意,可得:
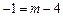 或
或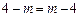 ,即
,即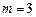 或
或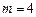 .……………………7分解析:
.……………………7分解析:略

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
 的方程
的方程 .
.
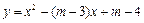 与
与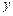 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求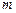 的值.
的值.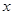 的方程
的方程
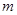 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)