题目内容
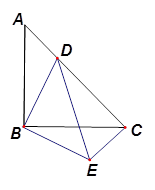
如图,等腰直角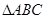 中,
中,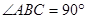 ,点
,点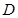 在
在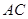 上,将
上,将 绕顶点
绕顶点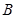 沿顺时针方向旋
沿顺时针方向旋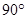 后得到
后得到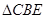 .
.
小题1:求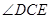 的度数
的度数
小题2:当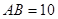 ,
,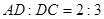 时,求
时,求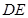 的长
的长
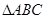 中,
中,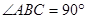 ,点
,点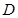 在
在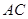 上,将
上,将 绕顶点
绕顶点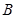 沿顺时针方向旋
沿顺时针方向旋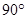 后得到
后得到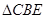 .
.
小题1:求
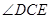 的度数
的度数小题2:当
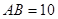 ,
,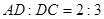 时,求
时,求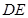 的长
的长小题1:∵
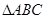 是等腰直角三角形
是等腰直角三角形∠A=∠ACB=45°
∵
 绕顶点
绕顶点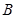 沿顺时针方向旋
沿顺时针方向旋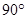 后得到
后得到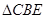 .
.∴∠BCE=45°
∴
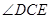 =∠ACB+∠BCE=45°+45°=90° (5分)
=∠ACB+∠BCE=45°+45°=90° (5分)小题2:∵
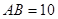
∴根据勾股定理可得AC=

∵
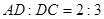
∴DC=
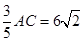 ,AD=
,AD=
∵
 绕顶点
绕顶点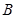 沿顺时针方向旋
沿顺时针方向旋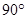 后得到
后得到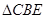 .
.∴CE=AD=

∵
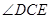 =90°
=90°根据韦达定理DE=
 =
= (9分)
(9分) (1)考查旋转后角的对应关系;(2)利用勾股定理来求出DE的长度。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;
; 的中点D顺时针旋转90°,画出相应的图形
的中点D顺时针旋转90°,画出相应的图形
 的路径的长度比点
的路径的长度比点 的路径的长度大 个单位.
的路径的长度大 个单位.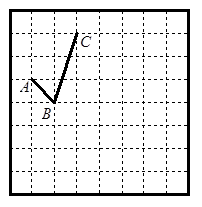


 (
( ),那么
),那么
 是从镜子中看到的, 它所对应的实际数字是 .
是从镜子中看到的, 它所对应的实际数字是 . 