题目内容
 如图,ABCD是平行四边形,E在AB上,F在AD上,S△BCE=2S△CDF=
如图,ABCD是平行四边形,E在AB上,F在AD上,S△BCE=2S△CDF=| 1 | 4 |
分析:可将三角形CEF的面积转化为四边形ABCD与几个小三角形的面积之差,进而求小三角形的面积即可.
解答:解:
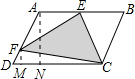
过点F、A作FM、AN垂直于DC,分别交BC于点M、点N,
∵S△BCE=
SABCD=2S△CDF=1,
∴SABCD=4,即CD•h=4,
又∵
BE•h=1,可得CD=2BE,即点E为AB的中点.
∴S△CDF=
S△BCE=
,即
CD•x=
,可得x=
h,
∴S△AEF=
•AE•(h-x)=
•
CD•
h=
,
∴S△CEF=SABCD-S△BCE-S△AEF-S△CDF=4-1-
-
=
.
故答案为:
.

过点F、A作FM、AN垂直于DC,分别交BC于点M、点N,
∵S△BCE=
| 1 |
| 4 |
∴SABCD=4,即CD•h=4,
又∵
| 1 |
| 2 |
∴S△CDF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴S△CEF=SABCD-S△BCE-S△AEF-S△CDF=4-1-
| 3 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
故答案为:
| 7 |
| 4 |
点评:本题主要考查三角形的面积计算,能够利用四边形的性质熟练解决此类问题.

练习册系列答案
相关题目
 13、如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
13、如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )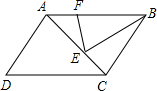 如图,ABCD是平行四边形,E在AC上,AE=2EC,F在AB上,BF=2AF,若△BEF的面积是2平方厘米,则平行四边形ABCD的面积是
如图,ABCD是平行四边形,E在AC上,AE=2EC,F在AB上,BF=2AF,若△BEF的面积是2平方厘米,则平行四边形ABCD的面积是 (2012•雅安)如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(2012•雅安)如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA. (2013•赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(
(2013•赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为( 如图,ABCD是平行四边形,∠DAB=α,AC是对角线.△ADC绕点A旋转β度角,得到△AD′C′,连结D′B.若△ABC≌△BAD′,试求出α与β的关系.
如图,ABCD是平行四边形,∠DAB=α,AC是对角线.△ADC绕点A旋转β度角,得到△AD′C′,连结D′B.若△ABC≌△BAD′,试求出α与β的关系.