题目内容
 如图,ABCD是平行四边形,∠DAB=α,AC是对角线.△ADC绕点A旋转β度角,得到△AD′C′,连结D′B.若△ABC≌△BAD′,试求出α与β的关系.
如图,ABCD是平行四边形,∠DAB=α,AC是对角线.△ADC绕点A旋转β度角,得到△AD′C′,连结D′B.若△ABC≌△BAD′,试求出α与β的关系.分析:根据旋转的性质得∠DAD′=β,则∠BAD′=β+α,再根据三角形全等的性质得到∠ABC=∠BAD′=α+β,然后根据平时四边形的性质得到∠DAB+∠ABC=180°,即α+α+β=180°,所以α与β的关系为α=90°-
β.
| 1 |
| 2 |
解答:解:∵△ADC绕点A旋转β度角,得到△AD′C′,
∴∠DAD′=β,
∴∠BAD′=∠DAD′+∠DAB=β+α,
∵△ABC≌△BAD′,
∴∠ABC=∠BAD′=α+β,
∵四边形ABCD是平行四边形,
∴∠DAB+∠ABC=180°,
∴α+α+β=180°,
即α=90°-
β.
∴∠DAD′=β,
∴∠BAD′=∠DAD′+∠DAB=β+α,
∵△ABC≌△BAD′,
∴∠ABC=∠BAD′=α+β,
∵四边形ABCD是平行四边形,
∴∠DAB+∠ABC=180°,
∴α+α+β=180°,
即α=90°-
| 1 |
| 2 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的性质.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 13、如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
13、如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )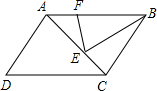 如图,ABCD是平行四边形,E在AC上,AE=2EC,F在AB上,BF=2AF,若△BEF的面积是2平方厘米,则平行四边形ABCD的面积是
如图,ABCD是平行四边形,E在AC上,AE=2EC,F在AB上,BF=2AF,若△BEF的面积是2平方厘米,则平行四边形ABCD的面积是 (2012•雅安)如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
(2012•雅安)如图,ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA. (2013•赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(
(2013•赤峰)如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上AD=OA=1,则图中阴影部分的面积为(