题目内容
已知二次函数y=-| 1 |
| 2 |
| 3 |
| 2 |
(1)求函数图象的顶点坐标和对称轴;
(2)求函数图象与坐标轴的交点坐标;
(3)画出此函数图象的草图,并根据图象回答:x为何值时,y>0?
分析:(1)利用公式直接解答或用配方法将原式化为顶点式解答;
(2)令x=0,求出与y轴交点坐标;令y=0,求出与x轴交点坐标;
(3)连接由(1)(2)求出的各点,即可画出草图.
(2)令x=0,求出与y轴交点坐标;令y=0,求出与x轴交点坐标;
(3)连接由(1)(2)求出的各点,即可画出草图.
解答: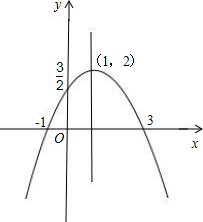 解:(1)原式可化为y=-
解:(1)原式可化为y=-
(x2-2x+1-1)+
=-
(x-1)2+2;
故顶点为(1,2),对称轴:直线x=1.
(2)当x=0时,y=
;则与y轴交点(0,
);
当y=0时,-
x2+x+
=0,
解得x1=-1,x2=3,
故与轴交点为(-1,0),(3,0).
(3)如图所示:
当-1<x<3时,y>0.
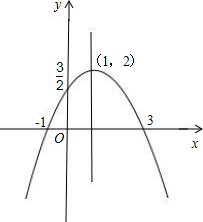 解:(1)原式可化为y=-
解:(1)原式可化为y=-| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故顶点为(1,2),对称轴:直线x=1.
(2)当x=0时,y=
| 3 |
| 2 |
| 3 |
| 2 |
当y=0时,-
| 1 |
| 2 |
| 3 |
| 2 |
解得x1=-1,x2=3,
故与轴交点为(-1,0),(3,0).
(3)如图所示:
当-1<x<3时,y>0.
点评:此题考查了二次函数与一元二次方程的关系,熟练掌握二次函数的表达式的各种形式及抛物线的性质是解题的关键.

练习册系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
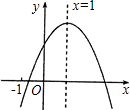 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: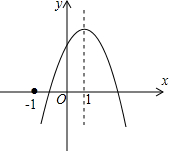 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;