题目内容
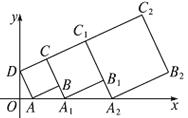
【题目】已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,它的两边分别交边
旋转,它的两边分别交边![]() 、
、![]() (或它们的延长线)于点
(或它们的延长线)于点![]() 、
、![]() .
.
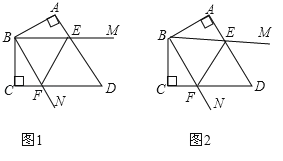
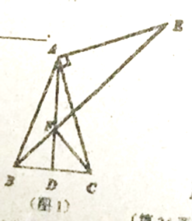
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),
时(如图1),
①求证:![]() ;
;
②求证:![]() ;
;
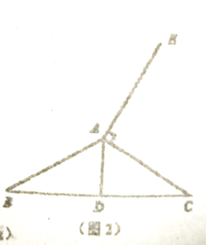
(2)当![]() 绕点
绕点![]() 旋转到如图2所示的位置时,
旋转到如图2所示的位置时,![]() ,此时,(1)中的两个结论是否还成立?请直接回答.
,此时,(1)中的两个结论是否还成立?请直接回答.
【答案】(1)①详见解析;②详见解析;(2)①不成立,②成立.
【解析】
(1)①根据AB=BC,∠A=∠C,AE=CF即可得证;
②先证△BEF为等边三角形,进而得到EF=BE=BF,再由![]() 结合
结合![]() ,
,![]() 可得
可得![]() ,进而可证得
,进而可证得![]() ,再用等量代换即可得证;
,再用等量代换即可得证;
(2)延长FC至G,使AE=CG,连接BG,先证△BAE≌△BCG,再证△GBF≌△EBF即可.
(1)①证明:![]() ,
,![]() ,
,
![]() .
.
在△ABE和△CBF中,

![]() (SAS).
(SAS).
②证明:由①知![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
(2)如图2,延长FC至G,使CG=AE,连接BG,
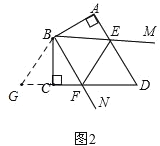
在△BAE和△BCG中,
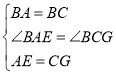 ,
,
∴△BAE≌△BCG(SAS),
∴∠ABE=∠CBG,BE=BG,
∵∠ABC=120°,∠EBF=60°,
∴∠ABE+∠CBF=60°,
∴∠CBG+∠CBF=60°,
∴∠GBF=∠EBF,
在△GBF和△EBF中,
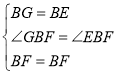 ,
,
∴△GBF≌△EBF(SAS),
∴EF=GF=CF+CG=CF+AE,
∴①不成立,②成立.

练习册系列答案
相关题目