��Ŀ����
��ͼ����ֱ֪��l1��y=-x+2��ֱ��l2��y=2x+8�ཻ�ڵ�F��l1��l2�ֱ�x���ڵ�E��G������AB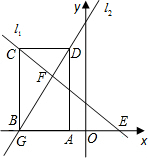 CD����C��D�ֱ���ֱ��l1��l2������A��B����x���ϣ��ҵ�B���G�غϣ�
CD����C��D�ֱ���ֱ��l1��l2������A��B����x���ϣ��ҵ�B���G�غϣ���1�����F������͡�GEF�Ķ�����
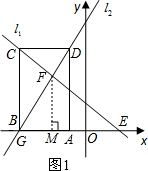
��2�������ABCD�ı�DC��BC�ij���
��3��������ABCD��ԭ�س�������x����������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ����ƶ�ʱ��Ϊt��0��t��6���룬����ABCD���GEF�ص����ֵ����Ϊs����s����t�ĺ�����ϵʽ����д����Ӧ��t��ȡֵ��Χ��
��������1������ֱ��l1��y=-x+2��ֱ��l2��y=2x+8�ཻ�ڵ�F���������������ʽ��ɷ�������ý⼴ΪF������꣮��F����ֱ��FM��ֱX�ύx����M��ͨ������ֵ��Ĺ�ϵ֤��ME=MF=4���Ӷ��õ���MEF�ǵ���ֱ�������Σ���GEF=45�㣻
��2���������B����G��������ꡢ��������õ�C��D��A�����꣮�������õ�DC��BC�ij���
��3�����Ƚ�����A��B��ʱ��t����ʾ���پ͢����˶���t�룬��BC����l2�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK�������˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK�������˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1���ཻ������������۽��s����t�ĺ�����ϵʽ��
��2���������B����G��������ꡢ��������õ�C��D��A�����꣮�������õ�DC��BC�ij���
��3�����Ƚ�����A��B��ʱ��t����ʾ���پ͢����˶���t�룬��BC����l2�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK�������˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK�������˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1���ཻ������������۽��s����t�ĺ�����ϵʽ��
��� �⣺��1���������
�⣺��1���������
��
���x=-2��y=4��
��F�����꣺��-2��4����
��F����ֱ��FM��ֱX�ύx����M��ME=MF=4����MEF�ǵ���ֱ�������Σ���GEF=45�㣻
��2���ߵ�G��ֱ��l2��x��Ľ��㣬
�൱y=0ʱ��2x+8=0�����x=-4��
��G�������Ϊ��-4��0������C��ĺ�����Ϊ-4��
�ߵ�C��ֱ��l1�ϣ�
���C��������-4��6����
����ͼ��֪��D���C����������ͬ���ҵ�D��ֱ��l2�ϣ�
���D��������-1��6����
����ͼ��֪��A���D�ĺ�������ͬ���ҵ�A��x���ϣ�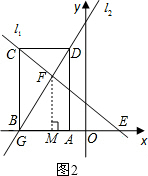
���A��������-1��0����
��DC=|-1-��-4��|=3��BC=6��
��3���ߵ�E��l1��x��Ľ��㣬
���E��������2��0����
S��GFE=
GE•MF=
(2+4)��4=12��
������ABCD��ԭ�س�������x����������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ�
��t��ʱ���ƶ��ľ�����1��t=t����B�������Ϊ��-4+t��0����A�������Ϊ��-1+t��0����
�����˶���t�룬��BC����l2�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK����ô-4��-4+t��-2����0��t��2ʱ��
N���������-4+t��2t����K���������-1+t��3-t����
s=S��GFE-S��GNB-S��AEK=12-
t•2t-
(3-t)•(3-t)=-
t2-3t+
��
�����˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK����ô-2��-4+t��-1+t��3����2��t��4ʱ��
N���������-4+t��6-t����K���������-1+t��3-t����
s=S����BNKA=
[(6-t)+(3-t)]•3=- 3t+
��
�����˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1���ཻ����ô-4+t��3��-1+t��3����4��t��6ʱ��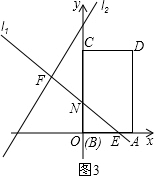
N���������-4+t��6-t����
s=S��BNE=
[2-(-4+t)]•(6-t)=
t2-6t+18��
�𣺣�1��F�����꣺��-2��4������GEF�Ķ�����45�㣻
��2������ABCD�ı�DC�ij�Ϊ3��BC�ij�Ϊ6��
��3��s����t�ĺ�����ϵʽ
��
 �⣺��1���������
�⣺��1���������
|
���x=-2��y=4��
��F�����꣺��-2��4����
��F����ֱ��FM��ֱX�ύx����M��ME=MF=4����MEF�ǵ���ֱ�������Σ���GEF=45�㣻
��2���ߵ�G��ֱ��l2��x��Ľ��㣬
�൱y=0ʱ��2x+8=0�����x=-4��
��G�������Ϊ��-4��0������C��ĺ�����Ϊ-4��
�ߵ�C��ֱ��l1�ϣ�
���C��������-4��6����
����ͼ��֪��D���C����������ͬ���ҵ�D��ֱ��l2�ϣ�
���D��������-1��6����
����ͼ��֪��A���D�ĺ�������ͬ���ҵ�A��x���ϣ�

���A��������-1��0����
��DC=|-1-��-4��|=3��BC=6��
��3���ߵ�E��l1��x��Ľ��㣬
���E��������2��0����
S��GFE=
| 1 |
| 2 |
| 1 |
| 2 |
������ABCD��ԭ�س�������x����������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ�
��t��ʱ���ƶ��ľ�����1��t=t����B�������Ϊ��-4+t��0����A�������Ϊ��-1+t��0����
�����˶���t�룬��BC����l2�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK����ô-4��-4+t��-2����0��t��2ʱ��
N���������-4+t��2t����K���������-1+t��3-t����
s=S��GFE-S��GNB-S��AEK=12-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 15 |
| 2 |
�����˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1�ཻ�轻��ΪK����ô-2��-4+t��-1+t��3����2��t��4ʱ��
N���������-4+t��6-t����K���������-1+t��3-t����
s=S����BNKA=
| 1 |
| 2 |
| 27 |
| 2 |
�����˶���t�룬��BC����l1�ཻ�轻��ΪN��AD��l1���ཻ����ô-4+t��3��-1+t��3����4��t��6ʱ��

N���������-4+t��6-t����
s=S��BNE=
| 1 |
| 2 |
| 1 |
| 2 |
�𣺣�1��F�����꣺��-2��4������GEF�Ķ�����45�㣻
��2������ABCD�ı�DC�ij�Ϊ3��BC�ij�Ϊ6��
��3��s����t�ĺ�����ϵʽ
|
������������һ�κ����������Ρ����Ρ��������ϵ����⣬��ͼ�������˶��Ĺ۵����п��о������ֵ����⣮

��ϰ��ϵ�д�
 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
�����Ŀ
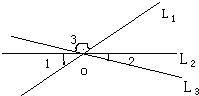 6����ͼ����ֱ֪��l1��l2��l3�ཻ�ڵ�O����1=35�㣬��2=25�㣬���3���ڣ�������
6����ͼ����ֱ֪��l1��l2��l3�ཻ�ڵ�O����1=35�㣬��2=25�㣬���3���ڣ�������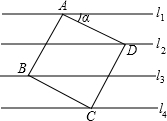 ��2012•۰����һģ����ͼ����ֱ֪��l1��l2��l3��l4����������ƽ��ֱ��ľ��붼��1�����������ABCD���ĸ�����ֱ�������ֱ���ϣ���cos��=��������
��2012•۰����һģ����ͼ����ֱ֪��l1��l2��l3��l4����������ƽ��ֱ��ľ��붼��1�����������ABCD���ĸ�����ֱ�������ֱ���ϣ���cos��=��������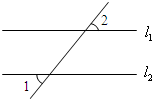 ��2007•ǭ���ݣ���ͼ����ֱ֪��l1��l2����1=50�㣬��ô��2=
��2007•ǭ���ݣ���ͼ����ֱ֪��l1��l2����1=50�㣬��ô��2=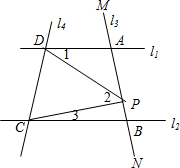 ��ͼ����ֱ֪��l1��l2����l3��l4��l1��l2�ֱ��ڵ�A��B�͵�C��D����P��AB�ϣ����ADP=��1����DPC=��2����BCP=��3��
��ͼ����ֱ֪��l1��l2����l3��l4��l1��l2�ֱ��ڵ�A��B�͵�C��D����P��AB�ϣ����ADP=��1����DPC=��2����BCP=��3�� ��ͼ����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C��D����ֱ��l3���е�P����P���C��D���غϣ�����A��ֱ��l1�ϣ���B��ֱ��l2�ϣ�
��ͼ����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C��D����ֱ��l3���е�P����P���C��D���غϣ�����A��ֱ��l1�ϣ���B��ֱ��l2�ϣ�