Ő‚ńŅńŕ»›
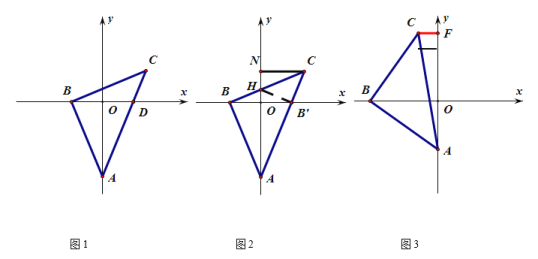
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ķ„A «y÷ŠłļįŽ÷Š…ŌĶń“ĽłŲ∂ĮĶ„£¨Ķ„B «x÷ŠłļįŽ÷Š…ŌĶń“ĽłŲ∂ĮĶ„£¨Ń¨Ĺ”AB£¨ĻżĶ„B◊ųABĶńīĻŌŖ£¨ ĻĶ√BC£ĹAB£¨«“Ķ„C‘ŕx÷ŠĶń…Ō∑Ĺ£ģ
£®1£©«ů÷§£ļ°ŌCBD£Ĺ°ŌBAO£Ľ
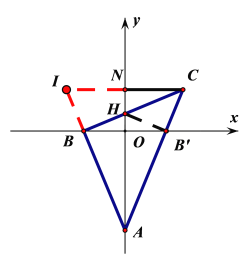
£®2£©»ÁÕľ2£¨Ķ„A°ĘĶ„B‘༨∂ĮĻż≥Ő÷–£¨į—AB—ōy÷Š∑≠’Ř ĻĶ√AB'ł’ļ√¬š‘ŕACĶńĪŖ…Ō£¨īň ĪBCĹĽy÷Š”ŕĶ„H£¨ĻżĶ„C◊ųCNīĻ÷Īy÷Š”ŕĶ„N£¨«ů÷§AH£Ĺ2CN£Ľ
£®3£©»ÁÕľ3£¨Ķ„A°ĘĶ„B‘༨∂ĮĻż≥Ő÷–£¨ ĻĶ√Ķ„C‘ŕĶŕ∂ĢŌůŌřńŕ£¨ĻżĶ„C◊ųCFīĻ÷Īy÷Š”ŕĶ„F£¨«ů÷§£ļOB£ĹAO+CF£ģ
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©ľŻĹ‚őŲ£Ľ£®3£©ľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›![]() £¨“‘ľį
£¨“‘ľį![]() Ņ…÷§√ų°ŌCBD£Ĺ°ŌBAO£Ľ
Ņ…÷§√ų°ŌCBD£Ĺ°ŌBAO£Ľ
£®2£©—”≥§CN°ĘABĹĽ”ŕĶ„I£¨łýĺ›’ŘĶĢĶń–‘÷ ÷™°ŌBAN£Ĺ°ŌCAN£¨‘ÚŅ…÷§√ų°ųCAN°’°ųIAN£¨‘Ú”–CN£ĹNI£¨‘Ŕ÷§√ų°ųICB°’°ųHAB£¨ľīŅ…Ķ√≥ŲAH£Ĺ2CN£Ľ
£®3£©ĻżC◊ųCJīĻ÷Īx÷Š£¨īĻ◊„ő™J‘ÚCJOFő™≥§∑Ĺ–ő‘ÚCF£ĹOJ£¨łýĺ›°ŌCBO+°ŌBCJ£Ĺ°ŌCBO+°ŌOBA£Ĺ900Ķ√≥Ų°ŌBCJ£Ĺ°ŌOBA£¨÷§√ų°ųCBJ°’°ųBAO£¨ľīŅ…÷§√ųOB£ĹOA+CF.
Ĺ‚£ļ£®1£©°Ŗ![]()
°ŗ°ŌCBD+°ŌDBA£Ĺ°ŌBAO+°ŌDBA£Ĺ900
°ŗ°ŌCBD£Ĺ°ŌBAO
£®2£©“Úő™AB—ōy÷Š∑≠’ŘŅ…÷™£¨
°ŌBAN£Ĺ°ŌCAN
—”≥§CN°ĘABĹĽ”ŕĶ„I£¨
‘ŕ°ųCANļÕ°ųIAN÷–
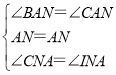
°ŗ°ųCAN°’°ųIAN£®ASA£©
°ŗCN£ĹNI
°ŗCI£Ĺ2CN
°ŖCN°Õy÷Š
°ŗ°ŌCNH£Ĺ°ŌCBA£Ĺ900
°ŌBHA£Ĺ°ŌNHC
°ŗ°ŌNCH£Ĺ°ŌBAH
‘ŕ°ųICBļÕ°ųHAB
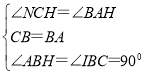
°ŗ°ųICB°’°ųHAB£®ASA£©
°ŗAH£ĹCI
°ŗAH£Ĺ2CN
£®3£©ĻżCĶ„◊ųCJīĻ÷Īx÷Š£¨īĻ◊„ő™J‘ÚCJOFő™≥§∑Ĺ–ő
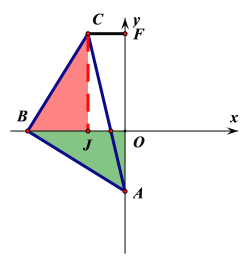
°ŗCF£ĹOJ
°Ŗ°ŌCBO+°ŌBCJ£Ĺ°ŌCBO+°ŌOBA£Ĺ900
°ŗ°ŌBCJ£Ĺ°ŌOBA
‘ŕ°ųCBJļÕ°ųBAO÷–
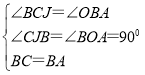
°ŗ°ųCBJ°’°ųBAO£®AAS£©
°ŗBJ£ĹOA
°ŖOB£ĹBJ+JO
°ŗOB£ĹOA+CF

 ”¶”√Ő‚ŐžŐžŃ∑ňńī®īů—ß≥Ųįś…ÁŌĶŃ–īūįł
”¶”√Ő‚ŐžŐžŃ∑ňńī®īů—ß≥Ųįś…ÁŌĶŃ–īūįł