题目内容
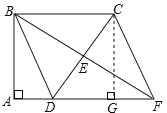
【题目】如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。

【答案】5![]() 或20.
或20.
【解析】
先证明四边形BDFC是平行四边形;当△BCD是等腰三角形求面积时,需分①BC=BD时,利用勾股定理列式求出AB,然后利用平行四边形的面积公式列式计算即可得解;②BC=CD时,过点C作CG⊥AF于G,判断出四边形AGCB是矩形,再根据矩形的对边相等可得AG=BC=5,然后求出DG=3,利用勾股定理列式求出CG,然后利用平行四边形的面积列式计算即可得解;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=4,矛盾.
证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
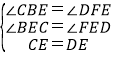
∴△BEC≌△FED,
∴BE=FE,
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(1)BC=BD=5时,由勾股定理得,AB=![]() =
=![]() =
=![]() ,
,
所以,四边形BDFC的面积=5×![]() =5
=5![]() ;
;
(2)BC=CD=5时,过点C作CG⊥AF于G,则四边形AGCB是矩形,
所以,AG=BC=5,
所以,DG=AG-AD=5-2=3,由勾股定理得,CG=![]() =
=![]() =4,
=4,
所以,四边形BDFC的面积=4×5=20;
(3)BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=4,矛盾,此时不成立;
综上所述,四边形BDFC的面积是5![]() 或20.
或20.
故答案为:5![]() 或20.
或20.

练习册系列答案
相关题目