题目内容
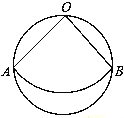
【题目】如图所示.点C，B 是线段 AD 上的两点， AC : CB : BD 3 :1: 4 ，点 E ， F 分别是 AB，CD 的中点，且 EF 14 ，求 AB，CD 的长.
【答案】AB=16，CD=20．
【解析】
根据已知条件“AC：CB：BD=3：1：4”设AC=3x，则CB=x，BD=4x，表示出BE，CF，根据EF=14列方程求解，即可得到x的值．从而求得线段AB、CD的长．
设AC=3x，则CB=x，BD=4x，∴AB=AC+CB=3x+x=4x，CD=CB+BD=x+4x=5x．
∵点E，F分别是AB，CD的中点则BE=
AB=2x，CF=CD=
．
∵EF=14，∴EB+CF-CB=14，∴
=14，解得：x=4，
∴AB=4x=16，CD=5x=20．
练习册系列答案
相关题目
【题目】某水果批发市场规定，一次购买苹果不超过100kg（包括100kg），批发价为5元，如果一次购买100kg以上苹果，超过100kg的部分苹果价格打8折．
（I）请填写下表
购买量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金额/元 | 0 | 250 | _ | 700 | __ | … |
（Ⅱ）写出付款金额关于购买量的函数解析式；
（Ⅲ）如果某人付款2100元，求其购买苹果的数量．
