Question

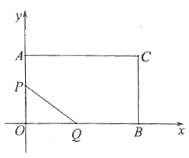
【题目】在平面直角坐标系中，已知点A(0，－2)、B(0，3)，点C是x轴正半轴上的一点，当∠BCA＝45°时，点C的坐标为__________________；

Answer 1

【答案】（+，0）

【解析】分析: 如解答图所示，构造含有90°圆心角的⊙P，则⊙P与x轴的交点即为所求的点C．

详解: 如图所示，作线段AB的中垂线l，交y轴于点M（，0），

在直线l上、y轴右侧取PM=MA=MB=，以点P为圆心、PA长为半径作圆，交x轴正半轴于点C，

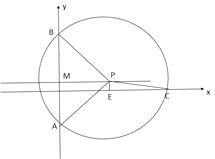
则PC=PA=PB=，

可知△PAB为等腰直角三角形，

由圆周角定理知∠BCA=∠BPA=45°，即点C即为所求；

∵PE=OM=，PM=OE=，

∴CE==，

∴OC=CE+OE=+，

此时点C坐标为（+，0）.

故答案为: （+，0）

点睛: 本题主要考查坐标与图形的性质，解题的关键是熟练掌握圆周角定理、勾股定理、等腰直角三角形的判定与性质