Question

【题目】已知O为直线AB上的一点，COE是直角，OF平分AOE（图中所说的角都是小于平角的角）.

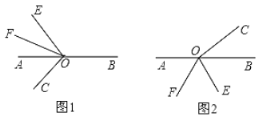
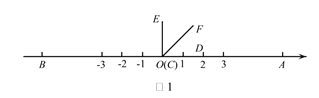
（1）如图1，若COF58°，求BOE的度数；

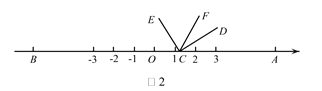
（2）将COE绕点O顺时针旋转到如图2所示的位置时，若COFm°，求BOE的度数（用含字母m的代数式表示）.

Answer 1

【答案】（1）116°；（2）360°﹣2m°．

【解析】

（1）根据互余得到∠EOF的度数，再由OF平分∠AOE，得到∠AOE=2∠EOF，然后根据邻补角的定义得到∠BOE的度数；

（2）当∠COF=m°，根据互余得到∠EOF=m°﹣90°，再由OF平分∠AOE，得到∠AOE=2∠EOF=2m°﹣180°，然后根据邻补角的定义得到∠BOE的度数，即可得到结论．

（1）∵∠COE是直角，∠COF=58°，∴∠EOF=90°﹣58°=32°．

∵OF平分∠AOE，∴∠AOE=2∠EOF=64°，∴∠BOE=180°﹣64°=116°．

故答案为：116°；

（2）∵∠COF=m°，∴∠EOF=m°﹣90°．

又∵OF平分∠AOE，∴∠AOE=2∠EOF=2m°﹣180°，∴∠BOE=180°﹣（2m°﹣180°）=360°﹣2m°．