题目内容
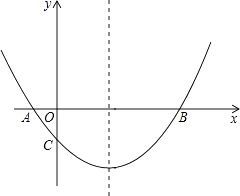
【题目】在平面直角坐标系中，直线y=﹣ 
x+1交y轴于点B，交x轴于点A，抛物线y=﹣ 
x2+bx+c经过点B，与直线y=﹣ x+1交于点C（4，﹣2）．
（1）求抛物线的解析式；
（2）如图，横坐标为m的点M在直线BC上方的抛物线上，过点M作ME∥y轴交直线BC于点E，以ME为直径的圆交直线BC于另一点D，当点E在x轴上时，求△DEM的周长．
（3）将△AOB绕坐标平面内的某一点按顺时针方向旋转90°，得到△A1O1B1 ， 点A，O，B的对应点分别是点A1 ， O1 ， B1 ， 若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的坐标．
【答案】
（1）
∵直线y=﹣ 
x+1交y轴于点B，
∴B（0，1），
∵抛物线y=﹣ 
x2+bx+c经过点B和点C（4，﹣2）．
∴ 
，
解得： 
，
∴抛物线的解析式为：y=﹣ x2+ 
x+1
（2）
如图1，
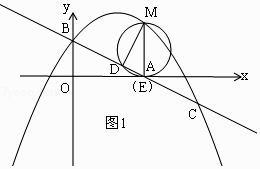
∵直线y=﹣ x+1交x轴于点A，
当y=0时，﹣ x+1=0，
x= 
，
∴A（ ，0），
∴OA= ，
在Rt△AOB中，
∵OB=1，
∴AB= 
，
∴sin∠ABO= 
，cos∠ABO= 
= 
，
∵ME∥x轴，
∴∠DEM=∠ABO，
∵以ME为直径的圆交直线BC于另一点D，
∴∠EDM=90°，
∴DE=MEcos∠DEM= ME，
DM=MEsin∠DEM= 
ME，
当点E在x轴上时，E和A重合，则m=OA= ，
当x= 时，y=﹣ × 
+ × +1= 
；
∴ME= 
，
∴DE= 
= 
，DM= 
= 
，
∴△DEM的周长=DE+DM+ME= + + = 
；
（3）
由旋转可知：O1A1⊥x轴，O1B1⊥y轴，设点A1的横坐标为x，则点B1的横坐标为x+1，
∵O1A1⊥x轴，
∴点O1，A1不可能同时落在抛物线上，分以下两种情况：
①如图2，当点O1，B1同时落在抛物线上时，
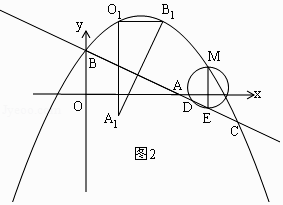
点O1，B1的纵坐标相等，
∴﹣ 
=﹣ （x+1）2+ （x+1）+1，
解得：x= ，
此时点A1的坐标为（ ， 
），
②如图3，当点A1，B1同时落在抛物线上时，
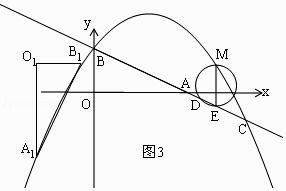
点B1的纵坐标比点A1的纵坐标大 ，
﹣ 
=﹣ （x+1）2+ （x+1）+1，
解得：x=﹣ 
，
此时A1（﹣ ， 
），
综上所述，点A1（ ， ）或（﹣ ， ）．
【解析】（1）利用待定系数法求抛物线的解析式；（2）如图1，A与E重合，根据直线y=﹣ x+1求得与x轴交点坐标可得OA的长，由勾股定理得AB的长，利用等角的三角函数得：sin∠ABO= ，cos∠ABO= = ，则可得DE和DM的长，根据M的横坐标代入抛物线的解析式可得纵坐标，即ME的长，相加得△DEM的周长；（3）由旋转可知：O1A1⊥x轴，O1B1⊥y轴，设点A1的横坐标为x，则点B1的横坐标为x+1，所以点O1 ， A1不可能同时落在抛物线上，分以下两种情况：①如图2，当点O1 ， B1同时落在抛物线上时，根据点O1 ， B1的纵坐标相等列方程可得结论；②如图3，当点A1 ， B1同时落在抛物线上时，根据点B1的纵坐标比点A1的纵坐标大 ，列方程可得结论．
【考点精析】利用圆周角定理和旋转的性质对题目进行判断即可得到答案，需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．
