Question

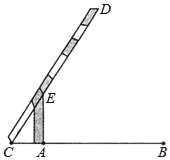
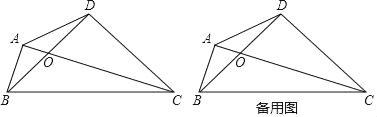
【题目】如图，四边形ABCD的对角线AC，BD相交于点O，OB＝OD，BD＝CD，∠BAC＝∠BDC＝90°．

（1）填空：∠ABD＝∠　 　；

（2）求的值；

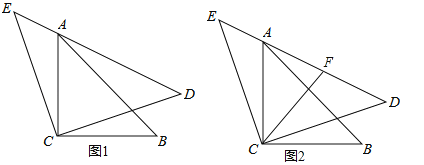
（3）点D关于直线BC的对称点为N，连接AN，请补全图形，探究线段AN，AD有怎样的关系，并加以证明．

Answer 1

【答案】（1）ACD；（2）；（3）AD⊥AN，．

【解析】

（1）因为∠BAC=∠BDC=90°，得到∠ABD+∠AOB=90°，∠ACD+∠COD=90°，根据等角的余角相等，即可得到∠ABD=∠ACD．

（2）作DH⊥OC于H．证明△BAO≌△DHO，根据全等三角形的性质得到AB=DH，设OD=OB=a，则BD=CD=2a，根据等面积法求出DH的长度，即可求出的值；

（3）连接BN、CN．根据△BDC是等腰直角三角形，得到D、N关于BC对称，有O′A=O′D=O′N=O′B=O′C，得到A、B、N、C、D五点共圆，根据圆周角定理得到∠AND=∠ACD，即可求出

解：（1）∵∠BAC=∠BDC=90°，

∴∠ABD+∠AOB=90°，∠ACD+∠COD=90°，

∵∠AOB=∠COD，

∴∠ABD=∠ACD．

故答案为ACD．

（2）作DH⊥OC于H．

∵∠BAO=∠DHO=90°，∠AOB=∠DOH，OB=OD，

∴△BAO≌△DHO，

∴AB=DH，设OD=OB=a，则BD=CD=2a，

∴

（3）结论：AD⊥AN，

理由：连接BN、CN．

∵△BDC是等腰直角三角形，

D、N关于BC对称，

∴四边形DBNC是正方形，设BC的中点为O′，连接O′N、O′A、O′D．

则有O′A=O′D=O′N=O′B=O′C，

∴A、B、N、C、D五点共圆，

∵DN是⊙O′的直径，

∴∠DAN=90°，

∴AD⊥AN，

∵∠AND=∠ACD，

∴tan∠AND=tan∠ACD，

∴