题目内容
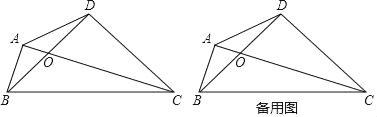
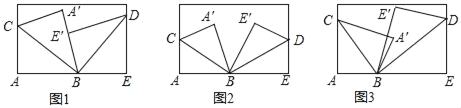
【题目】(1)将一张长方形纸片按如图1所示的方式折叠,BC、BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC、BD为折痕,若∠A′BE′=50°,求∠CBD的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC、BD为折痕,若∠A′BE′=α,请直接写出∠CBD的度数(用含α的式子表示)
【答案】(1)∠CBD=90°;(2)∠CBD=115°;(3)∠CBD=90°﹣![]() .
.
【解析】
(1)根据折叠的性质得到∠ABC=∠A′BC,∠EBD=∠E′BD,再根据平角的定义有∠ABC+∠A′BC+∠EBD+∠E′BD=180°,易得A′BC+∠E′BD=180°×![]() =90°,则∠CBD=90°;
=90°,则∠CBD=90°;
(2)根据折叠的性质得到∠A′BC=![]() ∠ABA′,∠DBE′=
∠ABA′,∠DBE′=![]() ∠EBE′,再根据平角的定义∠CBD=∠CBA′+∠DBE′+∠A′BE′=65°+50°=115°;
∠EBE′,再根据平角的定义∠CBD=∠CBA′+∠DBE′+∠A′BE′=65°+50°=115°;
(3)根据折叠的性质得到∠A′BC=![]() ∠ABA′,∠DBE′=
∠ABA′,∠DBE′=![]() ∠EBE′,再根据平角的定义∠CBD=
∠EBE′,再根据平角的定义∠CBD=![]() (∠ABA′+∠EBE′)﹣∠A′BE′.
(∠ABA′+∠EBE′)﹣∠A′BE′.
(1)由题意知∠ABC=∠A′BC,∠EBD=∠E′BD,,
∴∠A′BC=![]() ∠ABA′,∠E′BD=
∠ABA′,∠E′BD=![]() ∠E′BE,
∠E′BE,
∴∠CBD=![]() ∠ABE=90°;
∠ABE=90°;
(2)∵∠A′BE′=50°,
∴∠ABA′+∠EBE′=180°﹣∠A′BE′=130°,
∵∠A′BC=![]() ∠ABA′,∠DBE′=
∠ABA′,∠DBE′=![]() ∠EBE′,
∠EBE′,
∴∠CBA′+∠DBE′=![]() (∠ABA′+∠EBE′)=65°,
(∠ABA′+∠EBE′)=65°,
∴∠CBD=∠CBA′+∠DBE′+∠A′BE′=65°+50°=115°;
(3)∵∠A′BC=![]() ∠ABA′,∠DBE′=
∠ABA′,∠DBE′=![]() ∠EBE′,
∠EBE′,
∴∠CBA′+∠DBE′=![]() (∠ABA′+∠EBE′),
(∠ABA′+∠EBE′),
∴∠CBD=∠CBA′+∠DBE′﹣∠A′BE′=![]() (∠ABA′+∠EBE′)﹣∠A′BE′=
(∠ABA′+∠EBE′)﹣∠A′BE′=![]() (180°+α)﹣α=90°﹣
(180°+α)﹣α=90°﹣![]() .
.
故答案为:(1)∠CBD=90°;(2)∠CBD=115°;(3)∠CBD=90°﹣![]() .
.