��Ŀ����
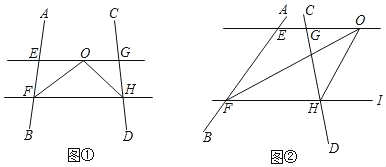
����Ŀ����̽������ͼ�٣���AFH�͡�CHF��ƽ���߽��ڵ�O��EG������O��ƽ����FH���ֱ���AB��CD���ڵ�E��G��
(1)����AFH��60������CHF��50�������EOF��_____�ȣ���FOH��_____�ȣ�
(2)����AFH+��CHF��100�������FOH�Ķ�����
����չ����ͼ�ڣ���AFH�͡�CHI��ƽ���߽��ڵ�O��EG������O��ƽ����FH���ֱ���AB��CD���ڵ�E��G������AFH+��CHF������ֱ��д����FOH�Ķ�����(�ú�a�Ĵ���ʽ��ʾ)
���𰸡���̽������1��30��125����2����FOH��130�㣻����չ����FOH��90�㩁![]() ����
����
��������
��1���ȸ��ݽ�ƽ���ߵĶ��������OFH����FHO �Ķ������ٸ��������ε��ڽǺͶ��������FOH�Ķ�����
��2���ȸ��ݽ�ƽ���ߵĶ��������OFH+��FHO �Ķ������ٸ��������ε��ڽǺͶ��������FOH�Ķ�����
����չ�� �ȸ��ݽ�ƽ���ߵĶ��������OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��![]() ��180��-��CHF�����ٸ�����ֱ��ƽ���ڴ�����ȵ���FOH����OHI����OFH���ɡ�
��180��-��CHF�����ٸ�����ֱ��ƽ���ڴ�����ȵ���FOH����OHI����OFH���ɡ�
��1���ߡ�AFH��60����OFƽ�֡�AFH��
���OFH��30����
�֡�EG��FH��
���EOF����OFH��30������ֱ��ƽ���ڴ����������
�ߡ�CHF��50����OHƽ�֡�CHF��
���FHO��25����
���FOH�У���FOH��180������OFH����OHF��125���������ε��ڽǺͶ�������
�ʴ�Ϊ��30��125��
��2����FOƽ�֡�AFH��HOƽ�֡�CHF��
���OFH��![]() ��AFH����OHF��
��AFH����OHF��![]() ��CHF��
��CHF��
�ߡ�AFH+��CHF��100����
���OFH+��OHF��![]() ����AFH+��CHF����
����AFH+��CHF����![]() ��100����50����
��100����50����
��EG��FH��
���EOF����OFH����GOH����OHF����ֱ��ƽ���ڴ��������.
���EOF+��GOH����OFH+��OHF��50����
�ߡ�EOF+��GOH+��FOH��180���������ε��ڽǺͶ�������
���FOH��180��������EOF+��GOH ����180����50����130����
��չ�ߡ�AFH�͡�CHI��ƽ���߽��ڵ�O��
���OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��
���FOH����OHI����OFH
��![]() ����CHI����AFH��
����CHI����AFH��
��![]() ��180������CHF����AFH��
��180������CHF����AFH��
��![]() ��180��������
��180��������
��90����![]() ����
����
��̽����
��1���ߡ�AFH��60�㣬OFƽ�֡�AFH��
���OFH��30�㣬
�֡�EG��FH��
���EOF����OFH��30�㣻
�ߡ�CHF��50�㣬OHƽ�֡�CHF��
���FHO��25�㣬
���FOH�У���FOH��180�㩁��OFH����OHF��125�㣻
�ʴ�Ϊ��30��125��
��2����FOƽ�֡�AFH��HOƽ�֡�CHF��
���OFH��![]() ��AFH����OHF��
��AFH����OHF��![]() ��CHF��
��CHF��
�ߡ�AFH+��CHF��100�㣬
���OFH+��OHF��![]() ����AFH+��CHF����
����AFH+��CHF����![]() ��100�㣽50�㣮
��100�㣽50�㣮
��EG��FH��
���EOF����OFH����GOH����OHF��
���EOF+��GOH����OFH+��OHF��50�㣮
�ߡ�EOF+��GOH+��FOH��180�㣬
���FOH��180�㩁����EOF+��GOH ����180�㩁50�㣽130�㣮
��չ�ߡ�AFH�͡�CHI��ƽ���߽��ڵ�O��
���OFH��![]() ��AFH����OHI��
��AFH����OHI��![]() ��CHI��
��CHI��
���FOH����OHI����OFH
��![]() ����CHI����AFH��
����CHI����AFH��
��![]() ��180�㩁��CHF����AFH��
��180�㩁��CHF����AFH��
��![]() ��180�㩁����
��180�㩁����
��90�㩁![]() ����
����