题目内容
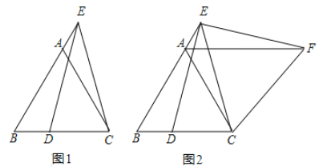
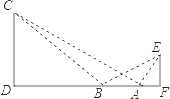
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
.
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
【答案】(1)旗杆EF的高为5![]() 米;(2)旗杆EF与实验楼CD之间的水平距离DF的长是45米
米;(2)旗杆EF与实验楼CD之间的水平距离DF的长是45米
【解析】
(1)根据题目中的数据和锐角三角函数可以求得EF和AF的长,从而可以解答本题;
(2)根据题目中的数据和锐角三角函数可以求得AD和AF的长,从而可以得到旗杆EF与实验楼CD之间的水平距离DF的长.
(1)解:∵∠EAF=60°,然后向左移动10米到B处,
测得∠EBF=30°,∠CBD=45°,tan∠CAD=![]() ,
,
∴tan60°=![]() ,tan30°=
,tan30°=![]() ,
,
解得,EF=![]() ,AF=5,
,AF=5,
即旗杆EF的高为![]() 米;
米;
(2)解:∵∠EAF=60°,然后向左移动10米到B处,
测得∠EBF=30°,∠CBD=45°,tan∠CAD=![]() ,AF=5,
,AF=5,
∴CD=BD,![]() ,
,
设CD=3a,则BD=3a,AD=4a,
∴AB=a=10,
∴BD=3a=30,
∴DF=AD+AF=40+5=45,
即旗杆EF与实验楼CD之间的水平距离DF的长是45米.

【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.